Négation critère de Cauchy

[Ssbb]

Bonjour, j’aimerai montrer que la série harmonique diverge en montrant que la suite des sommes partielle (Sn) n’est pas de Cauchy. Pour cela, je voudrais savoir si la négation du critère de Cauchy c’est bien ça ?

Il existe E>0, pr tout n ds N, il existe p,q ds N tq p,q>=n et |Sp-Sq|>=E

Est ce que c’est il existe p,q ou pr tout p, q
Car je ne sais pas si c’est
((Pr tt p,q p,q>=n) implique |Sp-Sq|<E)
Ou Pr tt p,q, (p,q>=n implique |Sp-Sq|<E)
À nier

Merci d’avance pour vos réponses

[GaBuZoMeu]

Bonjour,

Écris une phrase en français si tu te perds dans les formules
Le critère de Cauchy c'est que pour tout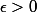 , il existe un entier naturel tel que pour tous entiers et , .
On peut en donner une version plus simple : pour tout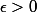 , il existe un entier naturel tel que pour tout entier , .

[tournesol]

Bonjour GaBuZoMeu
Je pense que tes phrases et en particulier la plus simple ne sont pas formalisées pour être niées de façon automatique . L'etudiant doit parfaitement connaitre la formulation formalisée.

Pour mémoire , la négation de est (P et nonQ)

[mathelot]

Bonjour,

critère de Cauchy


négation du critère de Cauchy


Appliqué à la série harmonique

[tournesol]

Oresme

[Ssbb]

Merci beaucoup pour vos messages, c’est très claire maintenant