mathelot a écrit:équation d'une droite ??
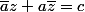
On peut arriver à cette forme en effet. Et même avec a de module 1.
mathelot a écrit:réflexion (symétrie axiale)

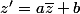
pour toute similitude indirecte.
Le cas des antidéplacements correspond à
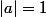
.
La particularité des réflexions (parmi les antidép) est que l'on a des points fixes. Ou bien que fof=Id.
En conséquence, toute droite a une équation du type
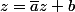
avec a de module 1. Si tu multiplies les deux membres par

où t=arg a, tuy retrouves l'équation de ta première question
mathelot a écrit:y-a-t-il une équation angulaire du cercle du style
=\alpha)
[

]
argument du quotient (z-a)/(z-b) tu veux dire? En ce cas oui. Car c'est l'angle (MA,MB). Bon si \alpha =0 on trouve une droite. A chaque fois privé de A(a) et de B(b) (à moins de faire des conventions projectives douteuses).
mathelot a écrit:l'inversion conserve globalement la réunion des droites et cercles ?
Il me semble bien.
mathelot a écrit:y a un rapport entre les homographies

et la géométrie projective ?
Dans un espace projectif de dimension quelconque, les homographies, c'est l'équivalent des applications linéaires inversibles pour les espaces vectoriels (ou des applications affines bijectives pour un espace affine). En dimension 2, les homographies sont ce que tu dis.
