MPSI : exo coniques
20 messages
- Page 1 sur 1
MPSI : exo coniques
Bonjour.
Voici une feuille d'exercices que j'ai à faire en DM pour lundi. http://img254.imageshack.us/img254/2401/imgqb.jpg
J'ai réussi le 1 et le 3.
Pour le 2, l'équation polaire de la tangente c'est pour moi (p/(1+ecosteta0)/cos(téta-téta0))
Or, ce corrigé dit que l'équation n'est pas celle que j'ai trouvé: http://mpsiddl.free.fr/pdf/Coniques%20-%20Equation%20polaire.pdf (les deux équations ne sont pas du tout équivalentes)
Pourriez-vous m'expliquer ce corrigé?
Pour l'exercice 4, j'ai donné les coordonnées de A, M, et N en fonction de leur ordonnées grâce à l'équation de la parabole.
Quand je fais AM scalaire AN = 0 j'obtiens quelque chose de très curieux, à savoir :
(ya²-yaS+P)(P+4p²+yaS+ya²)=0
Ca me donne soit l'un soit l'autre qui vaut 0. C'est correct? Comment poursuivre?
Je vais chercher l'exercice 5.
Merci de votre aide.
Voici une feuille d'exercices que j'ai à faire en DM pour lundi. http://img254.imageshack.us/img254/2401/imgqb.jpg
J'ai réussi le 1 et le 3.
Pour le 2, l'équation polaire de la tangente c'est pour moi (p/(1+ecosteta0)/cos(téta-téta0))
Or, ce corrigé dit que l'équation n'est pas celle que j'ai trouvé: http://mpsiddl.free.fr/pdf/Coniques%20-%20Equation%20polaire.pdf (les deux équations ne sont pas du tout équivalentes)
Pourriez-vous m'expliquer ce corrigé?
Pour l'exercice 4, j'ai donné les coordonnées de A, M, et N en fonction de leur ordonnées grâce à l'équation de la parabole.
Quand je fais AM scalaire AN = 0 j'obtiens quelque chose de très curieux, à savoir :
(ya²-yaS+P)(P+4p²+yaS+ya²)=0
Ca me donne soit l'un soit l'autre qui vaut 0. C'est correct? Comment poursuivre?
Je vais chercher l'exercice 5.
Merci de votre aide.
Salut,
Je sait pas si c'est censé être "connu" l'équation d'une tangente en polaire, mais, comme moi je connais pas, je repasse en cartésien :
=\rho(\theta)\cos\theta \cr y(\theta)=\rho(\theta)\sin\theta}\right. \Rightarrow <br />\left\{\matrix{x'(\theta) = \rho'(\theta) \cos\theta-\rho(\theta) \sin\theta\cr y'(\theta) = \rho'(\theta) \sin\theta+\rho(\theta)\cos\theta}\right.) donc la tangente en
donc la tangente en \cr y(\theta_o)}\right)) a pour équation cartésienne
a pour équation cartésienne &\ x'(\theta_o)\cr Y-y(\theta_o)&\ y'(\theta_o)\right|=0) c'est à dire
c'est à dire  X - x'(\theta_o) Y=\rho^2(\theta_o)\ \[=(xy'-x'y)(\theta_o)\]\ (*))
Pour avoir l'équation polaire de la tangente, il suffit donc d'écrire que et de déterminer
et de déterminer  en fonction de
en fonction de 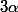 :
:
\ \Leftrightarrow\ <br />r\left(y'(\theta_o)\cos\alpha - x'(\theta_o)\sin\alpha\right)=\rho^2(\theta_o)\ <br />\Leftrightarrow\ <br />r=\frac{\rho^2(\theta_o)}{\sin(\theta_o-\alpha)\rho'(\theta_o)+\cos(\theta_o-\alpha)\rho(\theta_o) })
\right)'}{\rho^2}(\theta_o))
Et y'à plus qu'à appliquer tel le beuf (si je m'est pas gourré... :hein:)
Je sait pas si c'est censé être "connu" l'équation d'une tangente en polaire, mais, comme moi je connais pas, je repasse en cartésien :
Pour avoir l'équation polaire de la tangente, il suffit donc d'écrire que
Et y'à plus qu'à appliquer tel le beuf (si je m'est pas gourré... :hein:)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Visiblement, je me suis pas trop gourré, vu que je trouve comme la correction... :zen:
Sinon, pour le 4), tu n'as visiblement pas tenu compte d'un truc qui est sous entendu dans l'énoncé : vu qu'on parle des droites (AM) , (AN) et (MN), c'est que les trois points sont distincts...
Perso, en utilisant ce fait, je trouve comme équation (et je ne sais pas si ça correspond à ce que tu as trouvé vu que j'arrive pas trop à lire ta formule : utilise le MimeTeX)
(et je ne sais pas si ça correspond à ce que tu as trouvé vu que j'arrive pas trop à lire ta formule : utilise le MimeTeX)
Sinon, pour le 4), tu n'as visiblement pas tenu compte d'un truc qui est sous entendu dans l'énoncé : vu qu'on parle des droites (AM) , (AN) et (MN), c'est que les trois points sont distincts...
Perso, en utilisant ce fait, je trouve comme équation
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour l'exo 4, je trouve pareil que toi, sauf que j'ai un  en facteur de ton
en facteur de ton  et le tout qui fait 0.
et le tout qui fait 0.
J'en déduis que je dois justifier que n'est jamais nul. Si y_A est nul, alors Pi est non nul, et si y_A est non nul, alors la somme n'est pas nulle.
n'est jamais nul. Si y_A est nul, alors Pi est non nul, et si y_A est non nul, alors la somme n'est pas nulle.
Pour le 5, je crois que j'ai escroqué la question 1 et 2. Pour la 1 : J'ai appliqué f-1 de part et d'autre de l'égalité, j'obtiens f-1(B)=f-1(B)inter E. Et f-1(B) est inclus dans E.
J'en déduis que je dois justifier que
Pour le 5, je crois que j'ai escroqué la question 1 et 2. Pour la 1 : J'ai appliqué f-1 de part et d'autre de l'égalité, j'obtiens f-1(B)=f-1(B)inter E. Et f-1(B) est inclus dans E.
Tu t'est gourré dans tes calculs : le deuxième facteur (qui ne devrait pas apparaitre si tu avait simplifié par  et par
et par  plus tôt) doit évidement être :
plus tôt) doit évidement être :
(y_A-y_M)=y_A^2-y_A\sigma+\pi) vu que, pour obtenir ton truc, tu as écrit le produit scalaire des vecteurs AM et AN et que, trivialement, ce produit scalaire est nul lorsque M=A ou que N=A.
vu que, pour obtenir ton truc, tu as écrit le produit scalaire des vecteurs AM et AN et que, trivialement, ce produit scalaire est nul lorsque M=A ou que N=A.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour l'exercice 5), il n'y a pas vraiment d'astuce : c'est uniquement pour vérifier que tu arrive à utiliser les définitions de "image directe", "image réciproque", "injection", "surjection".
Tu peut à la rigueur faire des "patatoïdes" ou regarder sur un exemple de fonction f ce que ça donne mais ça ne donne pas forcément d'idée pour la preuve.
La seule chose un peu importante, c'est de voir que, comme on te demande de montrer que des ensembles sont égaux, si tu voit pas bien comment faire directement, tu peut procéder par double inclusion.
Tu peut à la rigueur faire des "patatoïdes" ou regarder sur un exemple de fonction f ce que ça donne mais ça ne donne pas forcément d'idée pour la preuve.
La seule chose un peu importante, c'est de voir que, comme on te demande de montrer que des ensembles sont égaux, si tu voit pas bien comment faire directement, tu peut procéder par double inclusion.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut ,
Pour le premier, je suis d'accord, ce n'est qu'une histoire d'application de définitions, en revanche pour la réciproque du 2 et 3 , il faut avoir l'idée - pas forcément naturelle - de considérer des ensembles bien choisis [mais pas "inhumains"] pour y parvenir, donc pas si "évident" que ça parfois ... :we:
Pour le premier, je suis d'accord, ce n'est qu'une histoire d'application de définitions, en revanche pour la réciproque du 2 et 3 , il faut avoir l'idée - pas forcément naturelle - de considérer des ensembles bien choisis [mais pas "inhumains"] pour y parvenir, donc pas si "évident" que ça parfois ... :we:
benekire2 a écrit:Salut ,
Pour le premier, je suis d'accord, ce n'est qu'une histoire d'application de définitions, en revanche pour la réciproque du 2 et 3 , il faut avoir l'idée - pas forcément naturelle - de considérer des ensembles bien choisis [mais pas "inhumains"] pour y parvenir, donc pas si "évident" que ça parfois ... :we:
Sans même (re)regarder le 2 et le 3, il me semble que "tes réciproques" concernent des implications du style :
"on sait des choses concernant les images directes/réciproques par f" et on veut en déduire "des choses concernant la fonction f elle même"
Alors, le truc qui semble quand même assez naturel, c'est de considérer les images directes/réciproques des singletons...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ouais, mais ça me semble pas totalement capilotracté de voir que, si tu connait la fonction "image directe par f" qui va des parties de A sur les parties de B, et que tu cherche à retrouver f, ben il suffit d'écrire que {f(x)}=f({x}) où le f de gauche est la "vrai" fonction f alors que celui de droite désigne la fonction "image directe" (c'est dans ce type d'exo qu'on se dit que c'est un peu chiant de noter les deux pareil : ça oblige à regarder ce qu'il y a comme argument pour savoir si c'est la fonction f ou la fonction "image directe")benekire2 a écrit:En effet , c'est ça :id: Mais si tu as jamais fait d'exo du style dans ta vie c'est pas évident je trouve ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si ça t'amuse ces exos sur les "images directes"/"images réciproque", tu peut chercher ça :
Soit A et B deux ensembles non vides et f:A->B une application. On note F:P(A)->P(B) l'application "image directe par f" et G:P(B)->P(A) l'application "image réciproque par f".
Déterminer toute les implications qu'il peut y avoir entre les 9 propriétées :
"f injective" , "f surjective" , "f bijective" , "F injective" , "F surjective" , "F bijective" , "G injective" , "G surjective" , "G bijective".
Soit A et B deux ensembles non vides et f:A->B une application. On note F:P(A)->P(B) l'application "image directe par f" et G:P(B)->P(A) l'application "image réciproque par f".
Déterminer toute les implications qu'il peut y avoir entre les 9 propriétées :
"f injective" , "f surjective" , "f bijective" , "F injective" , "F surjective" , "F bijective" , "G injective" , "G surjective" , "G bijective".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'espère quand même que tu sait écrire l'équation cartésienne d'une droite passant par deux points de coordonnées connues...
Donc, tu écrit ton équation, puis tu utilise les notations concernant sigma et pi ainsi que ce que tu as trouvé au 2a) pour n'avoir que les lettres p, yA et sigma dans ton éguation (avec évidement en plus un 'x' et un 'y' : c'est une équation de droite !!!)
Donc, tu écrit ton équation, puis tu utilise les notations concernant sigma et pi ainsi que ce que tu as trouvé au 2a) pour n'avoir que les lettres p, yA et sigma dans ton éguation (avec évidement en plus un 'x' et un 'y' : c'est une équation de droite !!!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
De nouveau (encore...) il faut voir que, comme l'énoncé parle de la droite (MN), il est sous entendu que M est différent de N et donc que yN est différent de yM.
Comme yN²-yM²=(yN-yM)(yN+yM), tu peut tout diviser par yN-yM et il te restera un yN+yM qui, comme par hasard, vaut sigma.
Comme yN²-yM²=(yN-yM)(yN+yM), tu peut tout diviser par yN-yM et il te restera un yN+yM qui, comme par hasard, vaut sigma.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tu t'est forcément gourré : pour écrire l'équation de la droite (MN) tu as écrit d'une façon ou d'une autre que c'était l'ensemble des points X tels que les vecteurs MX et MN soient colinéaires.Dubble a écrit:C'est fou, j'ai pi sigma a diviser par yn-ym, ça ne donne rien! ou alors j'ai fait une erreur de calcul. J'ai x+ y sigma/2p+pi sigma / (yn-ym)2p =0...
Sauf que, évidement, si M=N ça va marcher à tout les coups (quel que soit le point X) et cela signifie que, l'équation que tu doit trouver est forcément vérifiée lorsque yN=yM (quelque soient les autres valeurs) et donc que ton équation se divise parfaitement (i.e. sans fractions) par yN-yM.
Reprend tes calculs et regarde ligne par ligne si ton équation est vérifiée lorsque yN=yM. Si elle ne l'est pas... c'est que c'est faux...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Les points X:(x,y) situés sur la droite (MN) sont ceux tels que les vecteurs MX et MN soient colinéaires, c'est à dire tels que le déterminant  soit nul.
soit nul.
Vu le contexte, en factorisant
en factorisant  sur la première ligne et
sur la première ligne et  sur la deuxième colonne.
sur la deuxième colonne.
Comme on a donc :
on a donc :
(y_N+y_M)=0\ \Leftrightarrow\ <br />2px-(y_N+y_M)y +y_My_N=0)
Or et
et  donc on peut réécrire l'équation sous la forme :
donc on peut réécrire l'équation sous la forme :

Dans cette équation, lorsque M et N se baladent sur la parabole, il n'y a que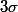 qui bouge et on cherche s'il n'y a pas des valeurs de
qui bouge et on cherche s'il n'y a pas des valeurs de  (dépendant de
(dépendant de  et de
et de  ) telles que l'équation soit vérifiée quelque soit
) telles que l'équation soit vérifiée quelque soit 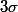 .
.
Il suffit d'écrire l'équation sous la forme :
+2px-y_A^2-4p^2=0)
pour voir que, si on prend et
et  alors l'équation sera vérifiée quelque soit la valeur de
alors l'équation sera vérifiée quelque soit la valeur de 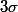
Vu le contexte,
Comme
Or
Dans cette équation, lorsque M et N se baladent sur la parabole, il n'y a que
Il suffit d'écrire l'équation sous la forme :
pour voir que, si on prend
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
