La monotonie d'une suite ...

par **rifly01** » 16 Nov 2007, 20:14

Bonjour,

J'ai un problème avec cet exercice :
[CENTER]

[/CENTER]

Voila ce que j'ai fait ...

a ) f est strictement croissante sur I et f(I) inclu dans I.
b) Je ne vois pas comment faire.
c) J'ai une partie de la réponse. D'après b) (u) est croissante (?) / Décroissante (?) de plus (u) est majorée / minorée donc convergente.
Pour déterminer la limite j'utiliserai le théorème du point fixe. En effet, il suffit de résoudre f(x)=0 et de prendre LA seule solution inclue dans I.

Merci, de me donner quelques indices.

par **busard_des_roseaux** » 16 Nov 2007, 21:13

Evaluer

(j'ai la flemme de faire le calcul).
Démonter que

sont héréditaires

par **yos** » 16 Nov 2007, 21:50

Sinon

.

par **busard_des_roseaux** » 16 Nov 2007, 21:53

yos a écrit:Sinon .

oui, c plus simple.

par **rifly01** » 16 Nov 2007, 23:10

Merci,

Pourquoi

?

Est-ce parce que

?

par **yos** » 17 Nov 2007, 10:50

donc tous les

sont dans I (récurrence triviale).

par **rifly01** » 17 Nov 2007, 12:14

Merci,

Pourquoi vous mettez la stricte inclusion ? "Tous les deux démarrent par ]0"

par **yos** » 17 Nov 2007, 12:22

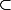
n'est PAS la stricte inclusion.

par **rifly01** » 17 Nov 2007, 14:28

C'est une simple inclusion ?
Mais alors, que veut bien dire

?

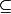
Comment note-t-on la stricte inclusion ?

merci,

par **yos** » 17 Nov 2007, 15:25

\subsetneq en Latex mais le site n'accepte que du Latex de base. Ca donne un

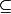
dont la partie inférieure est barrée.

La monotonie d'une suite ...

La monotonie d'une suite ...

Qui est en ligne