Moments d'inertie

[cdx01]

Bonjour, j'ai un problème avec un calcul de moment d'inertie. J'ai trois pièces assemblées, dont le calcul du moment d'inertie, calculé par mon logiciel de CAO, me donne une valeur de 0.083 Kg.m². Peut-être que je me trompe mais si je fais la somme du moment d'inertie de chaque pièce, je devrais trouver la même chose. Me trompe-je ?

Merci.

Cordialement.

[Robot]

Le moment d'inertie par rapport à quel axe ?
Par rapport à un axe fixé, le moment d'inertie de l'assemblage des trois est bien la somme des moments d'inertie de chacun. Mais comme tu oublies de parler des axes ...

[cdx01]

En effet je n'ai pas parlé d'axe. Mon logiciel de CAO m'a calculé le moment d'inertie de chaque pièce suivant un axe identique pour les trois pièces. Etant donné que mon ensemble n'est pas centré sur l'axe de symétrie, j'ai utilisé le théorème d'Huyguens. Je dois trouver, en fonction des 2 autres pièces, la masse de la 3ème pièce, pour ne pas dépasser un moment d'inertie maximum de 0.12 Kg.m². J'ai donc calculé le moment d'inertie de chacune des pièces et j'ai écris l'équation suivante :
(I1+I2+I3)+((M1+M2+M3)*d²)=0.12 Kg.m²

Je connais I1, I2 et I3 (M3/12*(b²+c²)) en fonction de M3, de b et c que je connais.

Mon problème réside dans le fait que je ne trouve pas le même résultat entre mon calcul et celui de mon logiciel CAO (auquel je fais confiance). Je ne trouve pas mon erreur.

[Robot]

Si tu veux qu'on te comprenne, il faudrait que tu sois plus explicite.
Tu n'introduis pas les notations que tu utilises. On imagine ce que son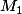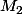t , et 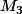, on ne sait pas par rapport à quels axes sont calculés 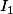, 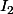et et 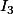on ne sait pas ce que sont , et .
Fais un effort de clarté.

[cdx01]

C'est bon, j'ai refait le calcul, je trouve le bon résultat. Merci quand même pour ton aide.

Cordialement.

[Robot]

Bon, on ne saura pas de quoi il retourne exactement. Tant pis.

[cdx01]

Robot, sais-tu si l'on peut-on envoyer une pièce jointe ? Ce serait plus simple qu'une explication compliquée.

Merci d'avance.

Cordialement.

[cdx01]

C'est bon j'ai trouvé comment joindre une image.

Sur l'image ci-jointe est représenté le sujet de mes messages. Tout n'est pas représenté, mais je ne peux pas en dévoiler plus. Cela permet de comprendre le principe.
L'ensemble pivote de 90° max. suivant l'axe X, vers l'avant, piloté par un moteur électrique.
Le but de mes messages était de trouver, en fonction des données de chaque pièce, la masse max. de la pièce verte pour ne pas dépasser un moment d'inertie de 0.12 Kg.m².

Cordialement.

[Robot]

Ca ne répond pas à mes questions. Mais puisque c'est couvert par le secret-défense, je n'insiste pas.

[cdx01]

I1 et I2 sont calculés suivant l'axe X. L'expression du moment d'inertie d'un parallélépipède est : M/12*(b²+c²). M est la masse de la pièce verte, b sa largeur et c son épaisseur.

d est la distance du centre de rotation au centre de gravité de l'ensemble (théorème d'Huyguens).

Donc l'expression totale du moment d'inertie est égal à : J=(I1+I2+(M3/12*(b²+c²)))+((M1+M2+M3)*d²).
I1, I2, b, c et d sont connus suivant l'axe X, reste juste à calculer M3 (masse de la pièce verte).