La méthodologie de résolution de la démonstion de sous-grp?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par LeFilsdeEinstein » 18 Déc 2021, 14:30
par LeFilsdeEinstein » 18 Déc 2021, 14:30
Bonjour,
Je me suis rencontré une difficulté durant la résolution d'un problème suivant:
Dans les exemples suivants, déterminer si la partie H est un sous-groupe de (G,*) 1.
 = (Z,+) et H := nombres paires)
2.
 = (Z,+) et H := nombres impaires)
3.
 = (R^*,\times) et H := ]-1, + \infty[)
Ma résolution:
1/
1.associativité
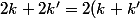)
donc k

(G,*)
2.élément neutre
Soit k est un élément neutre, alors
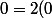)
donc k

(G,*)
3.commutativité
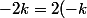)
donc k

(G,*)
Conclusion: H

(G,*)
2/
1.associativité
 + (2k'+1) =2 (k+k'+1))
donc k

(G,*)
2.élément neutre
Soit k est un élément neutre,
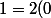+1)
donc k
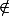
(G,*)
3.commutativité
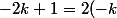+1)
donc donc k

(G,*)
Conclusion: H
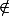
(G,*)
3/
1.associativité
pas tout les x , y , z
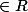
donc k
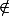
(G,*)
2.élément neutre

donc k

(G,*)
3.commutativité

Conclusion: H
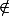
(G,*)
Si vous auriez des ressources supplémentaires à propos ce sujet, je vous remercie d'avoir indiqué.
Cordialement
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 18 Déc 2021, 15:00
par catamat » 18 Déc 2021, 15:00
Bonjour
Pour avoir un sous groupe H d'un groupe G muni de la loi *, on doit avoir les trois conditions suivante
Stabilité de H pour la loi *
L'élément neutre de * fait partie de H
L'inverse de tout élément de H pour la loi * fait partie de H
Les deux derniers ne sont pas stables, donner des contrexemples
Pour le premier
0=2*0 donc 0 est élément de H (c'est 0 l'élément neutre)
revoir la rédaction il ne s'agit pas d'associativité ni de commutativité
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 18 Déc 2021, 15:05
par catamat » 18 Déc 2021, 15:05
3.commutativité
-2k+1=2(-k)+1
donc k (G,*)
Il s'agit du troisième point que l'on peut rédiger ainsi :
Soit x élément de H, x=2k avec k dans Z
son inverse pour la loi * est ici son opposé -x
or -x=2(-k) avec (-k) dans Z donc -x est élément de H

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2021, 20:40
par Ben314 » 18 Déc 2021, 20:40
Salut,
catamat a écrit:...son inverse pour la loi * est ici son opposé...
Déjà que ça semble pas gagné concernant le concept de sous groupes pour LeFilsDeEinstein, autant utiliser correctement le vocabulaire :
Loi notée additivement -> OPPOSÉ
Loi notée multiplicativement -> INVERSE
Loi quelconque -> SYMÉTRIQUE
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2021, 14:47
par Ben314 » 19 Déc 2021, 14:47
Dans l'article sur les groupes (et pas celui sur les sous-groupes) la "remarque sur le vocabulaire" qui suit la définition dit bien la même chose que ce que j'ai mis.
J'ai pas lu en détail l'article sur les sous-groupes, mais je suppose que, comme c'est souvent le cas pour des groupes quelconques, l'article utilise les notations multiplicatives pour écrire les relations (donc, logiquement, il utilise le terme "d'inverse" pour désigner le symetrique)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 19 Déc 2021, 14:58
par catamat » 19 Déc 2021, 14:58
Ok
J'imaginais peut être qu'il s'agissait d'une traduction un peu rapide de l'article en anglais... en fait la définition de sous groupe que donne l'article est :
Soit H un sous-ensemble de G. On dit que H est un sous-groupe de (G, ∗) si la structure de G induit sur H une structure de groupe, c'est-à dire si les trois conditions suivantes sont satisfaites : H comprend le neutre de G, le composé de deux éléments de H selon la loi de G appartient toujours à H et l'inverse (selon la loi de G) de tout élément de H appartient lui-même à H. Dans ce cas, on dit aussi que le groupe formé par H et par la loi de groupe induite est un sous-groupe de G1.
en anglais cela donne ceci :
A subset H of the group G is a subgroup of G if and only if it is nonempty and closed under products and inverses
Ceci explique peut être cela... merci en tout cas d'avoir rétabli le mot français.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
