Méthode de newton et inégalité de Taylor Lagrange
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yonyon
- Membre Naturel
- Messages: 42
- Enregistré le: 25 Mai 2005, 17:48
-
par yonyon » 01 Mai 2006, 11:37
Bonjour, j'ai un problème avec cet exercice à la question b:
En appliquant l'inégalité de Taylor Lagrange, je trouve:
|f(b)-f(a)-(b-a)f'(a)|<M(b-a)²/2 mais je n'arrive pas à exprimer cela avec alpha et bêta. J'ai essayé de faire un dessin mais je ne vois pas trop comment faire :
j'ai f'(a)=f(a)/(bêta-a) mais c'ets tout....
Merci d'avance pour votre aide
-
mln
- Membre Relatif
- Messages: 131
- Enregistré le: 20 Avr 2006, 13:05
-
par mln » 01 Mai 2006, 13:13
Taylor Lagrange donne en a:
=f(a)+f'(a)(x-a)+\frac{1}{2}f''(u)(x-a)^{2})
avec u compris entre a et x
 = f(a)+f'(a)(\alpha-a)+\frac{1}{2}f''(u)(\alpha-a)^{2})
avec u entre a et
.
Or
=0)
Donc
+f'(a)(-\alpha +a)=\frac{1}{2}f''(u)(\alpha -a)^{2})
\neq 0)
}{f'(a)}-\alpha=\frac{f''(u)(\alpha-a)^{2}}{2f'(a)})
}{f'(a)})
(\alpha-a)^{2}}{2f'(a)})
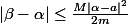
Or
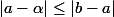
donc
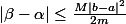
Je te laisse justifier selon tes théorèmes de Newton, point fixe...
Bon courage
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
