Maximum et minimum

[mehdi-128]

Bonjour,

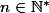
Soit . Montrer que toute partie à éléments de possède un maximum et un minimum.

Je tente le raisonnement par récurrence.

Initialisation : au rang tout partie à 1 élément est un singleton dont le max et le min sont égaux et valent l'élément qui appartient au singleton.

Hérédité : supposons que pour fixé on ait : possède un max et un min.

Montrons que : possède un max et un minimum avec

Et là je bloque

[Mimosa]

Bonjour

Compare et .

[mehdi-128]

Existence du maximum :
Si

Alors

Si

Alors

Existence du minimum :
Si

Alors

Si

Alors

C'est juste ?

[Mimosa]

Oui, mais tu peux prendre directement .

[mehdi-128]

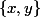
Dans l'exo précédent, j'avais démontré que pour 2 réels et l'ensemble possède un plus petit et un plus grand élément.

Mais je comprends pas trop votre indication avec le max du max car il faut partir de l'ensemble

[Mimosa]

C'est ce que j'ai fait. Relis attentivement!

[mehdi-128]

Ah j'ai compris il faut juste justifier que :

? Je vois pas trop comment faire.

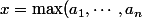Après on peut appliquer directement le résultat de l'exercice avec et

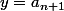
[aviateur]

Bonjour,

Initialisation : au rang tout partie à 1 élément est un singleton dont le max et le min sont égaux et valent l'élément qui appartient au singleton.

Bonjour, Peux tu démontrer cette affirmation?

[Ben314]

Salut,

Bonjour, Peux tu démontrer cette affirmation?

Je n'ai pas osé m'immiscer dans ce thread d'un niveau époustouflant, mais je plussoie des deux mains cette question essentielle d'aviateur...

[mehdi-128]

@Aviateur

Démontrer quelque chose d'évident ?

@Ben

Ca vous fait rire des gens qui essaient d'apprendre ?

Sinon je crois avoir réussi la démonstration.

Si je note

Si la maximum est atteint en pour

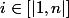
Alors :

Et

D'où l'égalité.

Si la maximum est atteint en

Alors :

Et

D'où l'égalité.

[beagle]

Salut,

Bonjour, Peux tu démontrer cette affirmation?

Je n'ai pas osé m'immiscer dans ce thread d'un niveau époustouflant, mais je plussoie des deux mains cette question essentielle d'aviateur...

salut Ben314, tu peux expliciter la subtilité derrière parce que pour un novice c'est pas parlant:
soit F= {a}
a est le maximum de F car pour tout y appartenant à F, on a:
y (inf -égal) a
ben pour tout y de F , y= a et on a bien a (inf-egal) a
et lycée de versailles pour minimum

Donc peut-être reformuler ce que vous demandez à mehdi-128, non?

[aviateur]

@ben314 Je te remercie d'avoir compris le sens caché de ma question.

[beagle]

ah la question était donc pour Ben314.

[beagle]

donc un forum d'échange en maths c'est l'endroit où les élèves posent des réponses incomprises par les profs, qui eux posent des questions incomprises par les élèves.
Un endroit convivial quoi!

[aviateur]

Bonjour

Sinon je crois avoir réussi la démonstration.
Si je note
Si la maximum est atteint en pour
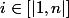
Alors :
Et
D'où l'égalité.
Si la maximum est atteint en
Alors :
Et
D'où l'égalité.

Bonjour, @medhi, Cela ne te gène pas d'utiliser l'existence du maximum pour montrer son existence?

[beagle]

non cela ne le gène pas car il ne dit pas que le maximum existe,
il dit s'il existait un maximum dans n éléments alors il existerait un maximum dans n+1 éléments
comme il existe un maximum pour un élément, alors c'est vrai pour deux éléments, pour 3 pour 4, … et là seulement cela devient vrai pour tout n dans le raisonnement de mehdi-128

donc peut-on repréciser l'endroit de son erreur de raisonnement?

[mehdi-128]

Bonjour

Sinon je crois avoir réussi la démonstration.
Si je note
Si la maximum est atteint en pour
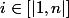
Alors :
Et
D'où l'égalité.
Si la maximum est atteint en
Alors :
Et
D'où l'égalité.

Bonjour, @medhi, Cela ne te gène pas d'utiliser l'existence du maximum pour montrer son existence?

C'était une récurrence donc dans l'hérédité j'avais pour n fixé :

existe

[beagle]

salut mehdi,
tu l'as écrit en sens inverse
soit le max des an est sup ou inf à a(n+1)
alors dans un cas on a un max pour n+1 qui est
max des an ou alors n+1
tu l'as écrit en sens inverse...

[mehdi-128]

Oui je vois mais du coup je ne sais pas répondre à la question d'Aviateur comment démontrer l'existence de :



C'est le serpent qui se mort la queue

[beagle]

Salut medhi, désolé je ne sais pas ce que les pros du site veulent te faire dire,
la récurrence n'est pas la bonne méthode ou bien ta façon de la rediger n'est pas la bonne,
cela ne répond que par énigmes, phrases lapidaires,
je décroche, j'espère que tu recevras des réponses un peu plus claires.

(sinon perso et c'est sans doute moins bien , mais les éléments je les ferais s'affronter deux par deux tels des gladiateurs, le plus faible serait éliminé à chaque fois,
resterait à la fin un élément et un seul qui n'aurait jamais perdu, c'est le max
mais il faut encore montrer que tous les chemins mènent au vainqueur, sont reliés …)

Bon courage à toi!