Bonsoir,
dans mon exercice de maths on me donne deux matrices A et P. Dans les premières questions j'ai du montrer que P est inversible puis j'ai calculé P^-1, j'ai ensuite calculé la matrice D=P^-1AP qui est diagonale et je dois à présent exprimer A en fonction de P, D et P^-1 sauf que je ne vois pas comment faire...
Pouvez-vous m'éclairer svp ?
Matrices
12 messages
- Page 1 sur 1
Re: Matrices
slt,
ben tu multiplies tlm à gauche par P
PD = PP^-1AP = IAP
puis tlm à droite par P^-1
ben tu multiplies tlm à gauche par P
PD = PP^-1AP = IAP
puis tlm à droite par P^-1
la vie est une fête 
Re: Matrices
Donc du coup j'obtiens PDP^-1=IAPP-1=2IA=A ?
Mais comment je peux justifier cette opération ?
Mais comment je peux justifier cette opération ?
Re: Matrices
Soit A=B.
JE multiplie à droite la matrice A par une matrice M : j'obitens AM.
Qu'est-ce que je peux dire de BM, sachant que A et B, c'est la même matrice (compte tenu de l'égalité) ?
PS.
C'est exactement la même chose quand au collège ou au lycée on manipule des égalités de nombres : quand on multiplie un membre, on multiplie l'autre membre par la même chose... La grosse différence avec les matrices, c'est la latéralisation car la multiplication n'est pas commutative.
Ceci dit, je ne comprends pas bien
D'où vient le "2I" ? Puis pourquoi le 2 disparaît ?
JE multiplie à droite la matrice A par une matrice M : j'obitens AM.
Qu'est-ce que je peux dire de BM, sachant que A et B, c'est la même matrice (compte tenu de l'égalité) ?
PS.
C'est exactement la même chose quand au collège ou au lycée on manipule des égalités de nombres : quand on multiplie un membre, on multiplie l'autre membre par la même chose... La grosse différence avec les matrices, c'est la latéralisation car la multiplication n'est pas commutative.
Ceci dit, je ne comprends pas bien
sasaaa84 a écrit:Donc du coup j'obtiens PDP^-1=IAPP-1=2IA=A ?
D'où vient le "2I" ? Puis pourquoi le 2 disparaît ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Matrices
Bonjour,
Pour compléter la problématique de hdci, il aurait fallu écrire
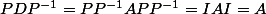
En règle général,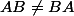 (c'est la non commutativité dont parle hdci même si dans le cas où
(c'est la non commutativité dont parle hdci même si dans le cas où 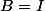 cela n'a pas d'importance) et de toute façon
cela n'a pas d'importance) et de toute façon 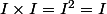 et en aucun cas
et en aucun cas  or je suis pratiquement certaine que c'est le raisonnement que tu as fais
or je suis pratiquement certaine que c'est le raisonnement que tu as fais
Pour compléter la problématique de hdci, il aurait fallu écrire
En règle général,
Re: Matrices
Oups c'est vrai j'ai écrit IAI=2IA ce qui est faux, merci !!
Merci hdci je n'avais pas bien compris cela, c'est beaucoup plus clair maintenant.
Merci hdci je n'avais pas bien compris cela, c'est beaucoup plus clair maintenant.
Re: Matrices
J'avais une autre question, comment montrer qu'une matrice de taille 3 est inversible ? Pour une matrice de taille 2 on calcule ad-bc mais pour une matrice de taille 3 je ne vois pas...
Re: Matrices
Tout dépend de ton programme (et donc de ta formation),
- si tu connais le déterminant, tu calcules le déterminant. S'il est non nul alors la matrice est inversible
- si tu ne connais pas le déterminant, tu commences le pivot de Gauss jusqu'à avoir une matrice triangulaire. Si tous ses coefficients diagonaux sont non nuls alors la matrice est inversible
- si tu connais le déterminant, tu calcules le déterminant. S'il est non nul alors la matrice est inversible
- si tu ne connais pas le déterminant, tu commences le pivot de Gauss jusqu'à avoir une matrice triangulaire. Si tous ses coefficients diagonaux sont non nuls alors la matrice est inversible
Re: Matrices
La théorie des déterminants existe pour toute matrice carrée, mais le calcul est "de plus en plus complexe". Et la règle reste la même : matrice inversible ssi le déterminant est non nul.
Il est encore relativement simple pour la matrice 3x3 : on fait la somme des produits des diagonales descendantes, moins, la somme des produits des diagonales montantes.
Sachant que par "diagonale", j'entends la diagonale principale, mais également celle par "complémentation" : ainsi
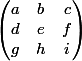
les trois diagonales descendantes sont (a,e,i), puis (b,f,g), puis (c,d,h)
les trois diagonales montantes sont (g,e,c), puis (h,f,a), puis (i,d,b)
Donc le déterminant est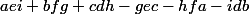
Il est encore relativement simple pour la matrice 3x3 : on fait la somme des produits des diagonales descendantes, moins, la somme des produits des diagonales montantes.
Sachant que par "diagonale", j'entends la diagonale principale, mais également celle par "complémentation" : ainsi
les trois diagonales descendantes sont (a,e,i), puis (b,f,g), puis (c,d,h)
les trois diagonales montantes sont (g,e,c), puis (h,f,a), puis (i,d,b)
Donc le déterminant est
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Matrices
Je n'ai pas vu le calcul du déterminant pour une matrice de taille 3, je vais donc utiliser la méthode du pivot de Gauss. Merci beaucoup à vous pour votre aide et bonne journée !!
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
