Matrices

[legendreuh]

Salut à tous,


Je bloque sur ce problème depuis un baille...

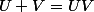
Soient telles que . Montrer que et commutent.

Voilà comment je m'y suis pris :

Si je montre le résultat pour inversible c'est fini, en effet : en utilisant la densité de dans et la continuité des applications et .

Seulement je n'arrive pas à aller plus loin, un coup de pouce ? Merci

[fatal_error]

salut,

jveux pas dire de boulettes mais l'addition est commutative:
U+V=V+U
donc UV=VU

donc la multiplication pour U et V est commutative non?

[MouLou]

Salut Legendreuh.

L'idée est d'utiliser cette relation en développant le produit de deux matrices bien choisies (à l'aide de U,V et la matrice identité). Cette relation te permettra de montrer que deux matrices sont inverses l'une de l'autre et donc commutent, ce qui entrainera la commutation de U et V.

Je te laisse chercher les matrices.

Pour ce qui est de la densité des matrices inversibles je vais y réfléchir

[Doraki]

salut,

jveux pas dire de boulettes mais l'addition est commutative:
U+V=V+U
donc UV=VU

donc la multiplication pour U et V est commutative non?

go home you're drunk.


U(1-V) = -V
Si V(x)=x alors 0 = -x, donc Ker(1-V) = {0}, et donc 1-V est inversible.
Soit W l'inverse de (1-V).
Alors V commute avec W (VW = WV (1-V)V = V(1-V) V-V² = V-V²)
et U = -VW, qui commute donc avec V.


avec l'indic de moulou c'est encore plus facile en fait XD

[alphamethyste]

salut

U+V=UV=VU

une solution simple

U=V=2I

en effet

U+V=UV
U^-1(U+V)=V
I+U^-1V=V

(U+V)V^-1=U
UV^-1+I=U

donc V=I+U^-1V et U=I+UV^-1

alors en posant U=V

V=I+U^-1V=I+I=2I
U=I+UV^-1=I+I=2I