Bonjour,
voila mon problème :
Données : S est l'ensemble des matrices symétrique de M(n,R) et A l'ensemble des matrices anti-symétriques de M(n,R).
S et A sont supplémentaires dans M(n,R).
Question : On prend n=3.
Trouver une base de S et une base de A.
Si quelqu'un peut m'aider, merci d'avance !
Matrices symétriques et antisymétriques
6 messages
- Page 1 sur 1
Le_chat a écrit:Salut.
Tu connais les dimensions de S et A?
Ensuite, c'est facile, tu trouves dim S matrices symétriques "élementaires" et dim A matrices antisymetriques, qui forment une famille libre.
Sinon, tu n'as pas vu de base de S et A dans le cas général?
Non je ne les connais pas, je dois les déduire dans la suite de l'exercice ...
Je n'ai pas vu non plus de base de S et A dans le cas général ; c'est en trouvant des bases pour n=3 que je devrais généraliser plus tard pour tout n non nul.
Ok ok.
Alors comment tu construit de manière simple une matrice symétrique:
1) Tu choisis les coefficients diagonaux.
2) Tu choisis les coefficients au dessus de la diagonale, et tu mets le même coefficient à la place 'transposée', en dessous de la diagonale.
Pour les matrice 3*3, c'est quoi la forme générale d'une matrice symétrique?
Alors comment tu construit de manière simple une matrice symétrique:
1) Tu choisis les coefficients diagonaux.
2) Tu choisis les coefficients au dessus de la diagonale, et tu mets le même coefficient à la place 'transposée', en dessous de la diagonale.
Pour les matrice 3*3, c'est quoi la forme générale d'une matrice symétrique?
Salut,
une matrice sumetrique de taille s'écrit
s'écrit  avec
avec  pour tout
pour tout  et
et  entre
entre  et
et  et
et  la matrice dont les entrées sont nulles sauf celle de la
la matrice dont les entrées sont nulles sauf celle de la  eme ligne et la
eme ligne et la  eme colonne, laquelle vaut
eme colonne, laquelle vaut 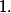 Ainsi :
Ainsi : 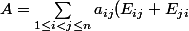 + \sum_{k=1}^n a_{kk} E_{kk})
J'espère que cela joint à ce qu 'a dit Le_chat ( ce n'est d'ailleurs qu'une traduction formelle de ce qu'i a dit) t suffit pour répondre à tes questions.
une matrice sumetrique de taille
J'espère que cela joint à ce qu 'a dit Le_chat ( ce n'est d'ailleurs qu'une traduction formelle de ce qu'i a dit) t suffit pour répondre à tes questions.
Bonsoir,
Voila la suite de mon problème :
Soit f l'application définie par f : M(n,R) -> M(n,R) avec f(M)=M+Mt
S est l'ensemble des matrices symétriques et A l'ensemble des matrices antisymétriques.
J'ai montré que f est une application linéaire et que Imf=A et Kerf=S.
On est maintenant dans le cas n=2.
Je viens d'écrire la matrice A de f relativement à la base canonique de M(2,R) et on me demande ensuite de calculer le rang de la matrice A ce que je n'arrive pas à faire ...
Je dois ensuite en déduire Imf, Kerf et conclure.
Merci d'avance
Voila la suite de mon problème :
Soit f l'application définie par f : M(n,R) -> M(n,R) avec f(M)=M+Mt
S est l'ensemble des matrices symétriques et A l'ensemble des matrices antisymétriques.
J'ai montré que f est une application linéaire et que Imf=A et Kerf=S.
On est maintenant dans le cas n=2.
Je viens d'écrire la matrice A de f relativement à la base canonique de M(2,R) et on me demande ensuite de calculer le rang de la matrice A ce que je n'arrive pas à faire ...
Je dois ensuite en déduire Imf, Kerf et conclure.
Merci d'avance
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
