Segment de matrices symétriques
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:09
par Nightmare » 19 Mar 2009, 18:09
Salut salut :happy3:
Toujours dans les matrices symétriques, voici un exercice intéressant auquel j'ai été confronté. J'ai ajouté une question mais je n'ai pas encore la réponse, je cherche en même temps que vous.
On se fixe deux matrices carrées symétriques réelles d'ordre n

et

telles que

.
On note
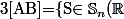, A\le S \le B\})
.
Montrer que

est un compact de
)
.
Question subsidiaire : Ce résultat marche-t-il si l'on remplace
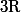
par un corps commutatif quelconque? Si non, trouver une CNS sur le corps pour que ce soit vrai.
amusez-vous bien.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Mar 2009, 18:16
par ThSQ » 19 Mar 2009, 18:16
Intéressant.
A <= B c'est bien B-A est positive ? Comment tu définis ça ailleurs que dans IR (ou dans C) ? Et tu mets quelle topologie ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:23
par Nightmare » 19 Mar 2009, 18:23
Bah, on a bien des formes hermitiennes positives non? :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:26
par Nightmare » 19 Mar 2009, 18:26
Oups désolé je n'avais pas vu ta modification !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:28
par Nightmare » 19 Mar 2009, 18:28
On pourrait définir la positivité sur des surcorps de R en disant que la forme est positive lorsqu'elle est à valeur dans R+.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:30
par Nightmare » 19 Mar 2009, 18:30
Pour la topologie, on peut prendre celle induite par la norme subordonnée multiplicative.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Mar 2009, 18:32
par ThSQ » 19 Mar 2009, 18:32
OK. J'ai cru que tu voulais parler de corps style Z/2Z ou autre corps non ordonné.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Mar 2009, 18:46
par ThSQ » 19 Mar 2009, 18:46
La fermeture est claire et la bornitude se déduit des inegs sur les vp non ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 18:54
par Nightmare » 19 Mar 2009, 18:54
Inégalité sur les vp? Je suis intéressé? Personnellement je suis plutôt parti sur l'existence d'une racine carré d'une matrice symétrique.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mar 2009, 19:16
par barbu23 » 19 Mar 2009, 19:16
Bonjour : :happy3:

ne peut -t-il pas s'ecrire comme ça :
B \hspace{3cm} | \hspace{3cm} t \in [0,1] \hspace{3cm} \} $)
? :hein:
Amicalement ! :happy3:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Mar 2009, 19:25
par yos » 19 Mar 2009, 19:25
barbu23 a écrit:
ne peut -t-il pas s'ecrire comme ça :
B \hspace{3cm} | \hspace{3cm} t \in [0,1] \hspace{3cm} \} $)
?
L'inclusion

semble claire mais l'autre?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Mar 2009, 19:31
par barbu23 » 19 Mar 2009, 19:31
Si on pose :
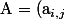_{1 \leq i,j \leq n} \in \mathcal{S} (\mathbb{R}^{n}) $)
:
Et si on considère la famille des projections continues

telle que :
 = a_{i,j} $)
Je pense que c'est facile d'y arriver ! non ? :hein:
Parceque, dans

:
,p_{i,j}(A)] = \{ \hspace{3cm} t.p_{i,j}(A) + (1-t) .p_{i,j}(A) \hspace{3cm} | \hspace{3cm} t \in [0,1] \hspace{3cm} \} $)
Amicalement ! :happy3:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Mar 2009, 20:03
par yos » 19 Mar 2009, 20:03
Prends A=diag(1,2), B=diag(3,5) et M=diag(2,3) dans
)
.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Mar 2009, 20:47
par ThSQ » 19 Mar 2009, 20:47
Nightmare a écrit:Inégalité sur les vp? Je suis intéressé? Personnellement je suis plutôt parti sur l'existence d'une racine carré d'une matrice symétrique.
Les vp sont entre celles de A et B + norme 2.
Ta soluce avec la C° de la racine carrée est très 'stucieuse ceci dit !
@barbu : c'est pas un segment au sens de la convexité mais c'est les matrices telles que A <= M <= B avec M <= N ssi N-M est positive.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 20:57
par Nightmare » 19 Mar 2009, 20:57
Peux-tu expliciter ta solution ThSQ? Je ne vois pas comment on pourrait conclure avec les vp...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 19 Mar 2009, 22:03
par ThSQ » 19 Mar 2009, 22:03
Xcuze c'est un peu décousu notre échange.
Dans le cas des matrices symétriques la rayon spectral coïncide avec la norme 2 et comme on peut prendre n'importe quelle norme !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Mar 2009, 22:07
par Nightmare » 19 Mar 2009, 22:07
Effectivement :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
et
telles que
.
.
est un compact de
.
par un corps commutatif quelconque? Si non, trouver une CNS sur le corps pour que ce soit vrai.
