Matrices semblables

[janor]

Bonjour! Voici mon problème:

Énoncé :

n>1
Jn est une matrice de taille n telle que tous ses coefficients sont nuls sauf ceux juste au dessus de sa diagonale qui valent 1. Jn est nilpotente d'indice de nilpotence n.
A est une matrice carrée de taille n nilpotente d'indice n.

rg(Jn^k)=n-k pour tout entier naturel k>0

E1 est une matrice de Mn,1(IK) telle que A^(n-1) ≠ 0
On a montré précédemment que: F = (A^(n-1)E1, A^(n-2)E1, ..., AE1, E1) est une base de Mn,1(IR)


Question : Montrer que A est semblable à Jn

Je cherche donc à montrer que A et Jn représentent le même endomorphisme dans 2 bases différentes de Mn,1(IR) : sa base canonique que j'ai noté B et la base F définie au dessus.
Seulement, ne connaissant pas A (je sais juste qu'elle est nilpotente d'indice n), je n'y arrive pas.

J'ai posé: A = MatB (u) et je veux montrer : Jn = MatF (u)
mais peut-être n'est-ce pas la bonne méthode ?

Désolée pour cet énoncé plutôt long et merci d'avance pour votre aide ^^

[GaBuZoMeu]

Bonsoir,

Soit ta base 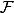. La matrice de l'endomorphisme dans la base 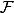est la matrice dont les colonnes sont les coordonnées de dans la base 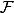(définition de la matrice d'un endomorphisme dans une base).