Matrices et fonction

[Manaus]

Bonjour bonjour à tous!!

J'ai une question d'un exercice que je n'arrive pas à résoudre.

Je dois trouver un minimum ou maximum local de cette fonction:


Je pense que c'est avec le gradient et la matrice hessienne que je dois résoudre cela mais je ne comprend pas comment ça fonctionne.

Si quelqu'un pouvait m'expliquer ou me donner de petites astuces pour résoudre ça, se serai déjà très apprécié.

Merci d'avance pour votre aide ! :we:

[capitaine nuggets]

Salut !

Bonjour bonjour à tous!!

J'ai une question d'un exercice que je n'arrive pas à résoudre.

Je dois trouver un minimum ou maximum local de cette fonction:


Je pense que c'est avec le gradient et la matrice hessienne que je dois résoudre cela mais je ne comprend pas comment ça fonctionne.

Si quelqu'un pouvait m'expliquer ou me donner de petites astuces pour résoudre ça, se serai déjà très apprécié.

Merci d'avance pour votre aide ! :we:

Déjà, est de classe comme fonction polynôme homogène de degré 2, donc en particulier, elle est deux fois dérivable.
Soit .
Alors on a deux cas :
1) Si et que la matrice hessienne est définie négative alors admet un maximum local (strict) au point .
2) Si et que la matrice hessienne est définie positive alors admet un minimum local (strict) au point .

La matrice hessienne (pourquoi ?) étant symétrique, je te rappelle que :
- est définie positive si pour toute matrice colonne non nulle à 3 éléments réels, on a .

[Manaus]

Merci beaucoup pour ta réponse!! Assez complexe tout ça mais je commence à comprendre.
Par contre pourrais-tu m'expliquer comment calculer et ?

[capitaine nuggets]

Merci beaucoup pour ta réponse!! Assez complexe tout ça mais je commence à comprendre.
Par contre pourrais-tu m'expliquer comment calculer et ?

Ok :

est la matrice dont les éléments sont de la forme (élément de la i-ième ligne et de la j-ième colonne).
Les varient dans avec et et (je les ai renommé parce que j'avais la flemme d'écrire cette matrice...)

[Manaus]

Ok :

est la matrice dont les éléments sont de la forme (élément de la i-ième ligne et de la j-ième colonne).
Les varient dans avec et et (je les ai renommé parce que j'avais la flemme d'écrire cette matrice...)

Merci pour ton aide!! je vais essayer de faire ça. J'aime pas les dérivées :hum:

[capitaine nuggets]

Merci pour ton aide!! je vais essayer de faire ça. J'aime pas les dérivées :hum:

N'hésite pas à revenir en cas de problèmes :+++:
Après, c'est une question de pratique : après en avoir fait 10 comme ça, t'auras fait le tour :ptdr:

[Manaus]

N'hésite pas à revenir en cas de problèmes :+++:
Après, c'est une question de pratique : après en avoir fait 10 comme ça, t'auras fait le tour :ptdr:

Bonsoir,

J'ai bien compris pour les calcules. J'arrive avec ça:


Mais après je n'ai pas compris comment les comparer et savoir si Hf est positif ou négatif.

[capitaine nuggets]

Salut !

Déjà, est de classe comme fonction polynôme homogène de degré 2, donc en particulier, elle est deux fois dérivable.
Soit .
Alors on a deux cas :
1) Si et que la matrice hessienne est définie négative alors admet un maximum local (strict) au point .
2) Si et que la matrice hessienne est définie positive alors admet un minimum local (strict) au point .

La matrice hessienne (pourquoi ?) étant symétrique, je te rappelle que :
- est définie positive si pour toute matrice colonne non nulle à 3 éléments réels, on a .

Bonsoir,

J'ai bien compris pour les calcules. J'arrive avec ça:


Mais après je n'ai pas compris comment les comparer et savoir si Hf est positif ou négatif.

Ok.
Dans le deux cas, on va être amené à étudier si est définie positive ou définie négative. Donc il faut prendre une matrice colonne à trois lignes et étudier le signe du réel .
Si tu as vu les formes bilinéaires, quadratiques, etc..., tu devrais pouvoir en déduire directement que :
.
Sinon fait le calcul :+++:
Une fois avoir prouvé que , étudie si c'est toujours strictement positif ou toujours strictement négatif :++:

[Manaus]

Il faut que je trouve les points critiques. Mais je n'arrive pas pour une fonction à 3 inconnus.
Et ensuite déterminer les valeurs propres de Hf pour chaque point pour savoir si c'est un minimum ou maximum, c'est ça?

[Manaus]

Merci!! Mais je comprend pas tout la...

Normalement selon mon prof. Après avoir trouvé le gradient et Hf je dois trouver les points critiques avec le gradient. Mais je n'arrive pas pour une fonction à 3 inconnus.

Et ensuite déterminer les valeurs propres de Hf et les comparer à 0 pour chaque point pour savoir si c'est un minimum ou maximum.

[capitaine nuggets]

Merci!! Mais je comprend pas tout la...

Normalement selon mon prof. Après avoir trouvé le gradient et Hf je dois trouver les points critiques avec le gradient. Mais je n'arrive pas pour une fonction à 3 inconnus.

Et ensuite déterminer les valeurs propres de Hf et les comparer à 0 pour chaque point pour savoir si c'est un minimum ou maximum.

Ben après ça dépend ce que tu as vu et de ce que je te propose :we:
Faisons ta méthode si tu veux :lol3:

Saurais-tu chercher les points critique du gradient ?

[Manaus]

Ben après ça dépend ce que tu as vu et de ce que je te propose :we:
Faisons ta méthode si tu veux :lol3:

Saurais-tu chercher les points critique du gradient ?

T'es vraiment gentil en tout cas merci :we:

Bah pour chercher les points critiques il faut trouver les valeurs possibles de x,y,z pour que les éléments du gradient soient nuls? Je l'ai déjà fait avec 2 variables mais 3 dans ce cas la je trouve pas.

[capitaine nuggets]

Bah pour chercher les points critiques il faut trouver les valeurs possibles de x,y,z pour que les éléments du gradient soient nuls? Je l'ai déjà fait avec 2 variables mais 3 dans ce cas la je trouve pas.

Ouais, à tout les coups, t'as dû voir une méthode assez particulièrement propre pour des fonctions de deux variables, mais avec trois variables, ce n'est plus la même chose :mur:

Déjà, trouver les points critiques de revient à résoudre .
Cela revient donc à résoudre le système de trois équations à trois inconnues (simple car toutes les variables ne sont pas présentes dans chaque équations) :

[CENTER] [/CENTER]

[Manaus]

Pour ma fonction ca me donne à résoudre.

Et je n'arrive pas... ou alors je me suis trompé dans les dérivés...

[capitaine nuggets]

Pour ma fonction ca me donne à résoudre.

Et je n'arrive pas... ou alors je me suis trompé dans les dérivés...

On peux le résoudre facilement à l'aide de la méthode du "pivot de Gauss" qui consiste à mettre le système sous une forme "triangulaire" (position des variables triangulaire). Je vais disposer les équations du système ainsi pour faciliter les calculs :+++:

[CENTER][/CENTER]

On ne touche plus à .
On veut ensuite supprimer les termes en " " dans l'équation .
Donc on retranche membre à membre à un multiple de tel qu'à la fin, on n'ait plus de termes en "". On a alors une nouvelle équation .
Une fois cela fait, on ne touche plus à et .
On veut enfin supprimer les termes en dans .
Donc on retranche membre à membre à un multiple de tel qu'à la fin, on n'ait plus de termes en "" (c'est possible car et n'ont que des termes en et ). On a alors une nouvelle équation .

Une fois cela fait, on aura un système de la forme :

[CENTER][/CENTER]

où sont tous réels que l'on va préciser (certains peuvent être nuls, mais là ça n'arrivera pas).
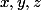
(Tu vois le "triange" formé par les variables maintenant :++:)


Si tu as compris, commence à résoudre le système :+++:

[Manaus]

Je suis entrain de le faire, ça devrait aller. J'avais pas pensé à ça mais c'est un peu comme trouver des inconnus avec la l réduite échelonnée d'un système linéaire mit sous forme matricielle :)

[capitaine nuggets]

Je suis entrain de le faire, ça devrait aller. J'avais pas pensé à ça mais c'est un peu comme trouver des inconnus avec la l réduite échelonnée d'un système linéaire mit sous forme matricielle

Ben en fait oui, c'est ça (deux noms pour une même chose quoi) ^^

[Manaus]

Comme souvent en maths ^^

[capitaine nuggets]

Comme souvent en maths ^^

Oui :ptdr:

Normalement, si je ne me suis pas trompé dans les calculs, tu devrais trouver (-3,-4,-3) comme unique solution (donc comme unique point critique).

[Manaus]

Okay c'est bon je trouvais pas comme toi mais je mettais trompé, je trouve pareil.

Maintenant faut que je trouve les valeurs propres de Hf en P(-3, -4, -3).



Comment on modifie Hf pour qu'il soit en P?