Matrices embêtantes

par **populo** » 04 Mar 2012, 19:13

Bonjour, j'essais depuis quelques jours à faire un exercice, mais je n'y arrive pas.
Le voici:
Les suites (xn), (yn) et (zn) sont solutions du système d'équations de récurrence:
( xn+1 = xn
<( yn+1 = yn - xn
( zn+1 = zn -yn
On écrira ce système sous la forme matricielle:
(xn+1)
Un+1 = (yn+1) = A x Un
(zn+1)
où 1 est une matrice qui peut se mettre sous la forme: A = I3 - N.
1) Calculer N^n pour n entier naturel. En déduire A^n.
Il y a d'autres questions mais déjà si on pouvait réussir à trouver une réponse à celle-ci, ce serai bien
merci.

par **Mortelune** » 04 Mar 2012, 19:42

Bonjour.

Déjà si tu écris la matrice A tu pourras voir que N est nilpotente.

par **populo** » 04 Mar 2012, 19:58

Matrice qui est égale à 0 dans une de ses puissances, ok.
Mais je ne comprend pas...
Ce que j'ai fais: remplacé A par I3 - N, ensuite j'ai donc (I3 . Un - N . Un) = ( xn )
(yn - xn)
(zn - yn)
puis apres quelques calculs, je suis à (x) (0)
N (y) = (xn)
(z) (yn)
ensuite?

par **Mortelune** » 04 Mar 2012, 20:33

Il faut que tu trouves A avec le système linéaire qui est donné, ensuite tu pourras faire ton exercice.

par **populo** » 04 Mar 2012, 21:34

Je n'y arrive même pas, je ne trouve pas N

par **Mortelune** » 04 Mar 2012, 21:38

Si tu n'as pas l'habitude de trouver une matrice à partir d'un système linéaire ça peut être normal que tu éprouves quelques difficultés.

La première colonne donneras les coefficients de

, la seconde ceux de

et la dernière ceux de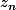

: ce résultat découle du produit matriciel qui est effectué.

Mais comme je le disais, avant de chercher N il faut trouver A.

par **populo** » 04 Mar 2012, 23:40

J'ai (xn ) (xn)
(yn-xn) = A x (yn), et ca donne koi?
(zn-yn) (zn)

par **populo** » 05 Mar 2012, 13:54

Petit up ^^

par **populo** » 05 Mar 2012, 18:19

? je n'y arrrive pas

par **Mortelune** » 05 Mar 2012, 19:22

.
Écris le produit matriciel et identifie les valeurs ...

par **populo** » 05 Mar 2012, 19:42

J'ai (xn ) (xn)
(yn-xn) = A x (yn), c'est bon?, ensuite je sais pas comment trouver A
(zn-yn) (zn)

par **Mortelune** » 05 Mar 2012, 19:43

Et si tu écris les différentes lignes du produit matriciel en fonction des suites x, y & z et des

ça donne quoi ... ?

par **populo** » 05 Mar 2012, 21:20

(xn) (i.xn)
(yn-xn) = (j.yn)
(zn-yn) (k.zn)

par **Mortelune** » 05 Mar 2012, 21:27

Tu n'avais jamais manipulé de matrices avant cet exercice ?

par **populo** » 05 Mar 2012, 21:55

il y à longtemps oui, mais c'est la 1ère fois depuis des années

par **Mortelune** » 05 Mar 2012, 21:56

Il faudrait peut être que tu regardes comment se fait le produit matriciel alors parce que là tu n'as pas l'air au point du tout :lol3:

Matrices embêtantes

Matrices embêtantes

re

re

re

re

Qui est en ligne