Matrice de transition

par **Adsederq** » 24 Juil 2005, 17:58

Quelqu'un pourrait m'aider avec une question qui me chicotte depuis un boute?
Bon voila, qu'es-ce que ca représente d'élever une matrice de transition au carré?
La matrice de transition est une matrice qui représente les changements de clientèles sur 1 ans de trois compagnie différentes dans une même région. On me demande d'élever la matrice au carré et ensuite de dire qu'es-ce que l'ont peut interpréter du terme Aij... La matrice est de formes 3x3. Les clients partent de J vers I. Je suis complèetement perdu? Si quelqu'un a une idée j'aimerais bien, et si vous voulez la matrice demandez moi c'est long a écrire et je doute qu'elle soit nécessaire mais bon... je peux tjrs l'ajouter éventuellement si nécessaire..merci D'avance :confused: :confused: :confused:

par **Chimerade** » 24 Juil 2005, 18:28

Adsederq a écrit:je peux tjrs l'ajouter éventuellement si nécessaire..merci

Je ne crois pas cela nécessaire. Par contre je visualise mal ce que contient la matrice

...

... est-elle une fraction comprise entre 0 et 1 représentant la proportion de clients de i partis chez j, de sorte que la somme

est forcément égal à 1 ?
Plus précisément, pour répondre à votre question, il faudrait un paramètre temporel : par exemple,

pourrait être la proportion de clients de i au 1-er janvier d'une année, qui se retrouvent clients de j au 31 décembre de la même année, mais ça pourrait aussi être la proportion de clients de i au 1-er Janvier d'une année, qui l'ont quitté pour j au moins une fois dans l'année, et qui ont pu éventuellement faire le chemin inverse dans le cours de l'année... Est-ce que l'élévation au carré de cette matrice correspond à une tentative de simulation de ce qui se serait passé au bout de deux ans si la matrice de la deuxième année est supposée identique à la matrice de la première ? Vous voyez ce que je veux dire ? Ce que je dis ressemble fort à des élucubrations sans queue ni tête, mais il faut comprendre que pour vous répondre il faut avoir davantage de précision sur la signification de cette matrice.

Bien évidemment, si quelqu'un est familier de ces matrices de transition, il pourra mieux que moi vous aider sans vous poser toutes ces questions bizarres ...

@+

par **Anonyme** » 24 Juil 2005, 18:49

(c'est 12h33!) :-)

(confère théorie des graphes)

Lorsqu'on élève la matrice de transition M au carré, le terme Aij de M² est égal au nombre de chemins de longueur 2 du graphe d'origine le sommet i et d'extrémité le sommet j.

à adapter donc.

par **Chimerade** » 24 Juil 2005, 19:05

Non inscrit a écrit:(c'est 12h33!)
Tiens bonjour ! O hisashiburi ! (en japonais, ça veut dire : Ca fait tellement longtemps qu'on ne s'était pas vus...)

Non inscrit a écrit:Lorsqu'on élève la matrice de transition M au carré, le terme Aij de M² est égal au nombre de chemins de longueur 2 du graphe d'origine le sommet i et d'extrémité le sommet j.

Ben je veux bien. J'attends quand même quelques éclaircissements de la part de Adsederk...

par **Adsederq** » 24 Juil 2005, 19:19

Bon voila je vais vous donnez l'énnoncer ca devrait éclaircir vos questionements :).
ON demande :
Trois câblodistributeurs C1, C2 et C3 desservent une région donnée. La matrice T suivante est une matrice de transition, où Tij représente la proportion de la clientèle du câblodistributeur j passant au câblodistributeurs i apres 1 année de service.
T=
0.6 0.5 0.3
0.2 0.3 0.3
0.2 0.2 0.4
Quelle interprétation peut-on donner à l'élément en position (i,j) de la matrice T² ?
:confused: :confused:
Mon T² donne :
0,52 0,51 0,45
0,24 0,25 0,27
0,24 0,24 0,28

en additionant les colones ensemble on obtien toujours 1. Donc je crois que T carré représente les clients apres deux ans de service, T au cube apres 3 ans et T^n apres n année de service? je suis correct?
Bien sur ca va se stabiliser mais je ne sais pas ou...et j'ai pas envhit de faire T^24 avant de nme rendre compte que c'est apres 18 ans!!!
quelqu'un a une idée pour ca (si le reste de ma déduction est correcte a tous le moins)... :eek: :cool:

par **Chimerade** » 24 Juil 2005, 22:35

Bon, je crois que j'ai compris. Ce que tu dis au sujet des matrices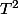

et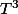

est tout-à-fait exact. Mais ne t'en fais pas, cela ne se stabilisera pas à

, vu que cela ne se stabilisera jamais. Disons que ça aura l'air de se stabiliser à peu près après un grand nombre d'itérations, mais sans jamais être parfaitement inchangé d'un coup sur l'autre.

Je ne sais pas quel est ton niveau d'études, mais pour résoudre ce problème il faut trouver les valeurs propres et les vecteurs propres de ta matrice. De cette manière tu verras mieux comment évolue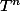

à mesure que n augmente.

Si tu sais ce que c'est (les valeurs propres et les vecteurs propres) et comment les calculer, fais-le. Sinon, tu ne peux qu'essayer de te faire une idée en continuant, disons une dizaine de fois. Tu peux aussi, si tu as le moyen d'écrire un programme sur ordinateur, essayer de lui faire calculer un grand nombre de fois, et voir...

par **Adsederq** » 25 Juil 2005, 05:08

OKay, mais meme si je ne vois pas pour T^n, je peux quand meme avoir une idée de s'que ca aura l'air avec n = 10 ?
Je vais essayer, je mettrai un signe de périodique dans le pire des cas -)
:D
Merci pour votre aide vous me sauver la vie !!

par **Anonyme** » 25 Juil 2005, 08:55

petite rectification:
lorsqu'on élève la matrice d'adjacence et pas de transition.

élever la matrice de transition à la puissance n, c'est obtenir l'état de ton système à l'étape n.

ce que tu as dit est correct donc.

un théorème dit que:
Si la matrice de transition P a tous ses coefficients strictement positifs, alors
la suite des matrices (P^m) converge vers une matrice stochastique dont les colonnes sont égales.

rq:
Une matrice stochastique est une matrice dont chacune des lignes est un
vecteur stochastique cad dont chaque élément est >=0 et de somme 1.

si tu cherches cet état limite : L=(X,Y,Z)
il vérifie (ça se démontre) LP=L
soit
L(I-P)=0
tu trouveras:
L=(1/2,1/4,1/4)

la matrice limite est:
P=
(1/2,1/2,1/2)
(1/4,1/4,1/4)
(1/4,1/4,1/4)

par **Anonyme** » 25 Juil 2005, 10:38

Non inscrit a écrit:petite rectification:
un théorème dit que:
Si la matrice de transition P a tous ses coefficients strictement positifs, alors
la suite des matrices (P^m) converge vers une matrice stochastique dont les colonnes sont égales.

la matrice limite est:
P=
(1/2,1/2,1/2)
(1/4,1/4,1/4)
(1/4,1/4,1/4)

Merci d'avoir pris le relais. Je ne pouvais rien dire de plus car je n'y connais rien, mais je crois que tu as conclu parfaitement le sujet.

par **Chimerade** » 25 Juil 2005, 12:17

Non inscrit a écrit:Merci d'avoir pris le relais. Je ne pouvais rien dire de plus car je n'y connais rien, mais je crois que tu as conclu parfaitement le sujet.

C'était moi ; j'ai encore oublié de m'identifier...

par **Chimerade** » 25 Juil 2005, 17:19

Non inscrit a écrit:la matrice limite est:
P=
(1/2,1/2,1/2)
(1/4,1/4,1/4)
(1/4,1/4,1/4)

Sans connaître les propriétés spécifiques de ce type de matrices, je me suis contenté de faire une vérification par programme. Je confirme que Non inscrit a tout à fait raison. De fait, la convergence est extrêmement rapide : à la précision de la machine près (53 bits donc 16 chiffres décimaux), la matrice devient stable entre

et

à partir de n=24 !

par **Adsederq** » 28 Juil 2005, 14:28

Reste que n = 24 c long...je l'ai fait pour n = 4 et j'ai déja une bonne idée a une décimal pres :P...j'ai pas de machine pour compter moi!! J'fais ca a la mitaine hehe :p

par **Chimerade** » 28 Juil 2005, 14:55

Adsederq a écrit:Reste que n = 24 c long...je l'ai fait pour n = 4 et j'ai déja une bonne idée a une décimal pres ...j'ai pas de machine pour compter moi!! J'fais ca a la mitaine hehe :p

Courage !

Si ça peux te consoler, de mon temps (avant la révolution !), on n'avait pas droit aux calculatrices, parce que tout simplement ça n'existait pas ! On faisait tous nos calculs, soit avec une règle à calcul, soit avec une table de logarithmes (je l'ai gardée, ma table de log Bouvard et Ratinet !)

Si cela t'intéresse, je peux t'envoyer le résultat de mon programme...24 matrices de 9 nombres avec 16 chiffres de précision...

par **Adsederq** » 29 Juil 2005, 16:55

Oui j'aimerais bien...es-ce que tu utilise maple ou matematica ou es-ce que c'est autre chose?

par **Chimerade** » 29 Juil 2005, 17:18

Adsederq a écrit:Oui j'aimerais bien...es-ce que tu utilise maple ou matematica ou es-ce que c'est autre chose?

J'ai écrit un petit programme en C.

Je t'envoie les resultats dans un message privé, pour ne pas encombrer le forum.

@+

Matrice de transition

Matrice de transition

Qui est en ligne