Matrice !!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 21 Nov 2005, 00:18
par Anonyme » 21 Nov 2005, 00:18
Bonsoir tout le monde !
J'ai moi aussi mon petit problème avec un exercice !
Le voici :
Soient

des nombres réels.
Considerons la matrice
M=

Le but de cet exercice est de calculer le déterminant de M.
Soit

Soit E =
_{1\leq ij\leq n})
la matrice définie par
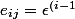(j-1)})
On pose P(X)=

a) Montrer que pour tout

{0,1,...,n-1} et tout

on a
i}+a_{0}\epsilon^{(n-k)i}+a_{1}\epsilon^{(n-k+1)i}+...+a_{k-1}\epsilon^{(n-1)i}=\epsilon^{(n-k)i}P(\epsilon^{i}))
b)Calculer ME de façon élégante en utilisant le polynome P (pas besoin de justifications...)
c)Montrer que le calcul de det(ME) se ramène par des opérations simples au calcul de det E.
d)En déduire que det M sous forme d'un produit des valeurs de P.
-
Anonyme
 par Anonyme » 21 Nov 2005, 00:18
par Anonyme » 21 Nov 2005, 00:18
Merci d'avance pour votre aide !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Nov 2005, 15:10
par yos » 21 Nov 2005, 15:10
a) factorise le premier membre par epsilon^(n-k)i. Utilise le fait que
epsilon^n= 1 pour faire apparaitre P(epsilon^i).
b) Déf du produit de 2 matrices : le calcul de la question a) donne le terme de la matrice ME ligne n-k+1 modulo n, colonne i+1 modulo n.
c)factorise le déterminant de ME par le produit des P(epsilon^i) ( dans la colonne i+1 , tu as P(epsilon^i) en facteur de chaque terme.
d)det(ME)=det(M)det(E) et det(E) est un Vandermonde. On en déduit la valeur de det(M).
J'espère que mes indices sont corrects. Bon courage
-
ras
- Messages: 1
- Enregistré le: 21 Nov 2005, 19:18
-
 par ras » 21 Nov 2005, 19:26
par ras » 21 Nov 2005, 19:26
je n'ai pas lu entierement ton exo
mais normalement cela se fait avec la matrice circulante, J
des 0 partout sauf sur la sur-diagonale
alors ta matrice vaut sigma( ai*J^i)
je voulais demander qqch
est ce que qqn peut m'indiquer ou se trouve le site lesmaths.net
MERCI
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
