Matrice stochastique

par **yos** » 31 Mai 2007, 17:28

Bonjour. Voilà un joli exercice d'algèbre linéaire.
On appelle matrice stochastique d'ordre n, une matrice M telle que

(On dit stochastique strict si les

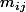
sont >0.)
On note S l'ensemble des matrices stochastiques d'ordre n.

Soit donc

Démontrer que S est fermé pour la multiplication.
Démontrer que
Démontrer que 1 est vp de M.
Démontrer que si est une vp complexe de M, alors .
Soit une vp de module 1. Démontrer que est une racine de l'unité.

PS . Je sais pas faire la dernière question sauf pour une stochastique stricte.
Pour la question 2, ne pas tricher en utilisant la question 4.

par **mehdi-128** » 31 Mai 2007, 17:38

Bonjour, http://perso.orange.fr/gilles.costantini/prepas_fichiers/matstoch.pdf

par **Daniel-Jackson** » 31 Mai 2007, 17:45

Très bon exo , je m erappelle à l'oral pour montrer la stabilité par produit , je m'étais lancé dans des calculs un peu barbares qui donent le résultat mais il suffisait de remarquer qu'une matrice ("positive" ) est stochastique si et seulement si le vecteur 1 = ( 1,...,1) est vecteur propre. Après c'est assez technique . Bref c'est exactement ce qui est fait dans le lien que mehdi-128 a donné là .

par **yos** » 31 Mai 2007, 17:46

En voilà des façons Mehdi! Et ceux qui ont envie de chercher alors?
A noter que
1) la question que je sais pas faire est pas évoquée sur ton lien.
2) les autres y sont résolues de manière bien poussives.

par **mehdi-128** » 31 Mai 2007, 17:48

désolé ,mais toute aide n'est-elle pas la bien venue? :)

par **yos** » 31 Mai 2007, 17:49

Daniel-Jackson a écrit:Très bon exo , je m erappelle à l'oral pour montrer la stabilité par produit , je m'étais lancé dans des calculs un peu barbares qui donent le résultat mais il suffisait de remarquer qu'une matrice ("positive" ) est stochastique si et seulement si le vecteur 1 = ( 1,...,1) est vecteur propre. Après c'est assez technique . Bref c'est exactement ce qui est fait dans le lien que mehdi-128 a donné là .

Euh non ils le font de manière directe il me semble. Mais c'est vrai qu'on pourrait inverser les questions.

par **yos** » 31 Mai 2007, 17:50

mehdi-128 a écrit:désolé ,mais toute aide n'est-elle pas la bien venue?

Si! je ralais par principe (comme Gavrilo hum!)

par **fahr451** » 31 Mai 2007, 18:38

tous ces résultats sont intéressants et classiques dans l 'étude des chaines de markov élémentaires

par **mehdi-128** » 31 Mai 2007, 18:41

Ok :) ......

par **Daniel-Jackson** » 31 Mai 2007, 19:04

yos a écrit:Euh non ils le font de manière directe il me semble. Mais c'est vrai qu'on pourrait inverser les questions.

Non je parlais des question d'après ... pas de la stabilité

par **yos** » 31 Mai 2007, 19:38

Daniel-Jackson a écrit:Non je parlais des question d'après ... pas de la stabilité

Ah OK
Dans le lien de Mehdi-

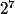
(propriété 4), on parle de vp dominante. Savez-vous ce que c'est.
Cette propriété 4 me donne une idée pour finir l'exercice (peut-être).

par **Daniel-Jackson** » 31 Mai 2007, 20:22

yos a écrit:Ah OK
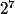
Dans le lien de Mehdi- (propriété 4), on parle de vp dominante. Savez-vous ce que c'est.
Cette propriété 4 me donne une idée pour finir l'exercice (peut-être).

A mon avis valeur propre dominante c'est la plus grande en module ...sans doute strictement plus grande , mais je suis pas sûr
Je réfléchis et j'esaie de faire la question recalcitrante , j'ai fait cet exo y'a un bon bout de temps je vais m'y mettre là

par **Joker62** » 31 Mai 2007, 21:29

Hello

Sympa cet exo, et en plus il a l'air courant, donc bon autant s'y intéresser en plus m'ennui

Donc j'ai déjà fait la 1)

Soit

deux matrices stochastiques de dimension n
Montrons que

i) On a clairement que tous les éléments de C sont positifs ou nul étant donné que c'est la somme de terme positifs.

ii) On a

Posons

les lignes de C.

Vérifions que

Donc S est fermé par multiplication

Edit : j'viens de regardé la solution, pi j'ai même pas triché.

par **yos** » 31 Mai 2007, 21:42

Joker62 a écrit:Posons les lignes de C.

Vérifions que

Ces

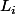
que tu additionnes c'est bizarre. Tu t'es emmelé dans les indices , mais c'est un détail. Après c'est tout bon.

par **Joker62** » 31 Mai 2007, 21:47

Oui j'voulais dire Li désigne la ligne i et ensuite sommer sur j les Lij :)
J'continue la suite c'est sympathique :)

par **BiZi** » 31 Mai 2007, 21:53

Bonjour,

Un indice: pour la 5), ca devient relativement simple si on reprend le raisonnement de la 4) :happy2:

par **BiZi** » 31 Mai 2007, 22:02

yos a écrit:Bonjour. Voilà un joli exercice d'algèbre linéaire.
On appelle matrice stochastique d'ordre n, une matrice M telle que
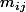
(On dit stochastique strict si les sont >0.)
On note S l'ensemble des matrices stochastiques d'ordre n.

Soit donc
Démontrer que S est fermé pour la multiplication.
Démontrer que
Démontrer que 1 est vp de M.
Démontrer que si est une vp complexe de M, alors .
Soit une vp de module 1. Démontrer que est une racine de l'unité.

PS . Je sais pas faire la dernière question sauf pour une stochastique stricte.
Pour la question 2, ne pas tricher en utilisant la question 4.

Euh je crois que ca marche pas si la matrice est seulement stochastique.

par **yos** » 31 Mai 2007, 22:11

BiZi a écrit:Euh je crois que ca marche pas si la matrice est seulement stochastique.

Ah? C'est pourtant la question dans un exo d'oral de l'X.
Le cas que j'ai appelé stochastique strict est pas intéressant car je ne trouve que 1 et -1 comme vp de module 1 (sauf erreur de raisonnement).

par **fahr451** » 01 Juin 2007, 15:01

la question 4 est évidente et donne la 2 de façon immédiate j'appelle pas ça tricher mais être astucieux

la 5 est dure
soit a vp de module 1 a différente de 1 et X un vecteur propre complexe associé

MX = a X

en prenant yi réalisant ll Xll inf on en déduit

sigma mij xj = a xi puis en passant au module

l xi l =< sigma mij l xjl =< sigma mij l xi l = l xil
donc égalité dans l 'inégalité triangulaire les complexes mij xi sont sur une demi droite engendrée par un z

pour tout j : mij xj = ai z avec ai positif puis on voit que

pour j et k vérifiant mij et mik non nuls on a xj = xk

puis xj = a xi

ce qui impose mii = 0
on pose j(0) = i
on prend un indice j(1) avec mij(0) non nul on a

y(j(1)) = a y(j(0)) et puisque l y(j(1) l = l y(j0)l
on recommence avec j(1) au lieu de j(0) on trouve j(2) tel que
y(j(2)) = ay(j(1)) etc
on conclut avec les chaussettes dirichleiennes

il existe j(k) et j(k+p) égaux p>0

y(j(k+p)) = a^p y(j(p)) soit a^p = 1

par **yos** » 01 Juin 2007, 20:26

Merci Fahr pour cette réponse.
Ma remarque sur la question 2 tient au fait qu'on peut faire ça par récurrence dés qu'on connait la notion de déterminant. C'est facile en élargissant l'hypothèse de la façon suivante :

(je trouve que c'est pas évident d'y penser).

Pour la question 5, j'avais commencé pareil et c'est pourquoi je trouvais le résultat si je supposais que les

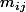
sont tous non nuls. Je vois en gros la suite de ce que tu as fait à un ou deux détails près qu'il faudra que j'écrive.

Sais-tu si avec n=3 on a des exemples où les vp sont 1,i,-i ou 1,j,-j par exemple ?

Matrice stochastique

Matrice stochastique

Qui est en ligne