bonjour
pour eclaircir un point du cours:
j'ai la matrice M=
0 0 -1
1 0 0
0 1 0
M est elle diagonalisable? si oui donner une matrice semblable
je trouve que -1 est la valeur propre d'ordre de multiplicite 1
(donc la matrice n'est pas diagonalisable)
mais est ce que je peut dire qu'elle est semblable -I(3)
et donc dire que m^3 = -I(3)
Matrice semblable
6 messages
- Page 1 sur 1
ça tu pouvais le voir sans aucun calcul. En effet, le théorème de Cayley-Hamilton te dit que 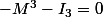 .
.
En fait, je ne pense pas que cela suffit pour conclure que c'est une ta matrice est semblable ... cependant on peut continuer et vérifier si elle est symétrique. tu as vraiment mis tout l'énoncé en haut ?
Pour montrer que deux matrices sont semblables il faut montrer que les deux matrices représentent un endomorphisme dans deux bases différentes.
Donc je pense que ton exercice fait intervenir des bases.
--------------
Je trouve que ces deux matrices et
et  sont semblables.
sont semblables.
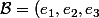) et
et 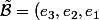)
En fait, je ne pense pas que cela suffit pour conclure que c'est une ta matrice est semblable ... cependant on peut continuer et vérifier si elle est symétrique. tu as vraiment mis tout l'énoncé en haut ?
Pour montrer que deux matrices sont semblables il faut montrer que les deux matrices représentent un endomorphisme dans deux bases différentes.
Donc je pense que ton exercice fait intervenir des bases.
--------------
Je trouve que ces deux matrices
je suis en premiere anne je me rapelle pas du theoreme de Cayley-Hamilton
l'enonce donne la matrice en
1- demande de calculer le polynome caracteristique je trouve:-X^3-1
2- la matrice M est elle diagonalisable sur R? sur C?si oui indiquer une matrice semblable diagonale(on ne demande pas le calcul des espaces propres
3-determiner M^3
l'enonce donne la matrice en
1- demande de calculer le polynome caracteristique je trouve:-X^3-1
2- la matrice M est elle diagonalisable sur R? sur C?si oui indiquer une matrice semblable diagonale(on ne demande pas le calcul des espaces propres
3-determiner M^3
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
