Longueur d'arc
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 01 Avr 2016, 11:26
par Ncdk » 01 Avr 2016, 11:26
Bonjour,
Soit

un arc géométrique paramétré par
)
.
Soit
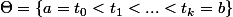
une subdivision de

=\sum_{i=0}^{k-1} ||f(t_{i+1})-f(t_i)||)
et
 = \sup_{\Theta} l(f,\Theta) \in [0,+\infty])
Je voulais savoir à quoi peut bien servir cette définition, car on a une définition qui se manipule très bien, celle avec l'intégrale, enfin ma phrase est pas adéquat, je dirais plutôt, dans quels cas on peut se servir de cette définition, notamment en géométrie différentielle.
Merci

-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 01 Avr 2016, 13:24
par lionel52 » 01 Avr 2016, 13:24
Déjà une definition avec l'intégrale ne serait pas intuitif pour calculer la longueur d'une courbe alors que la definition que tu proposes est "logique" Au fur et à mesure que tu rajoutes des points sur ton chemin, le chemin et la distance parcourue s'approchera de plus en plus de celui de la courbe réelle.
Maintenant en pratique pour le calcul c'est la definition avec l'intégrale qui est utilisée en priorité

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 01 Avr 2016, 14:17
par Ncdk » 01 Avr 2016, 14:17
Oui en effet, il me semble aussi qu'on se sert de ces subdivisions pour définir l'intégrale de Riemann, avec des fonctions en escaliers il me semble, ça y ressemble beaucoup non ?

-
Ben314
- Le Ben
- Messages: 21704
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2016, 17:35
par Ben314 » 01 Avr 2016, 17:35
Sans parler du fait que, contrairement à la soit disant définition (qui n'en est pas une...) avec une intégrale, celle là a le bon gout de ne demander absolument aucune régularité à la fonction f (ni C1, ni C1 par morceaux, ni même dérivable et même... ni même continue...)
Donc c'est évidement LA définition qu'il faut prendre (i.e. le cas le plus général possible) quitte à ensuite trouver des CAS PARTICULIER (par exemple dans le cas où f est continue et C1 par morceaux) où on peut calculer la longueur avec autre chose que la définition (évidement après avoir démontré que c'était bien la même valeur que ça donne)
C'est uniquement avec cette définition là que tu peut par exemple calculer la longueur d'une courbe fractale et montrer qu'elle est infinie vu qu'en général une courbe fractale n'est nulle part dérivable.
Et je "plussois" ce que dit Lionel, à savoir que cette définition est de très loin la plus intuitive qui soit : ça me semble complètement contre intuitif de décréter que seules les courbes ayant des tangentes (presque) partout possèdent une "longueur" vu que je vois pas de rapport entre le fait "d'admettre des tangentes" et celui de "posséder une longueur".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
