Arc géométrique et longueur d'arc
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 21 Jan 2017, 11:58
par Ncdk » 21 Jan 2017, 11:58
Bonjour,
Je dois montrer que tout arc géométrique A régulier et C^1 admet un paramétrage par longueur d'arc.
Soit
)
un paramétrage régulier de

et soit
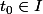
.
On pose
 = \int_{t_0}^t ||f'(u)||du)
.
On sait que pour tout
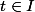
,
 \ne 0)
. La fonction

est

et sa dérivée est strictement positive.
Il s'agit donc d'un

-difféomorphisme de

sur

où
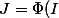)
Soit
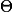
sa fonction réciproque qui est

et qui va de

dans

.
On pose
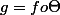
et on doit montrer que
'(s)||=1)
Du coup
=(fo\Theta)'(s)=f'(\Theta(s)).\Theta'(s)=f'(t).\Theta'(s))
Je suis bloqué ici en fait, je sais pas comment exprimer
)
en fonction de t.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2017, 12:42
par Ben314 » 21 Jan 2017, 12:42
Salut,
Ncdk a écrit:Je suis bloqué ici en fait, je sais pas comment exprimer
)
en fonction de t.
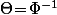
(bijection réciproque) donc
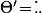
Si tu ne connait pas la formule, il suffit de dériver l'égalité
\!=\!s)
(valable sur l'intervalle

) pour la retrouver.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 21 Jan 2017, 13:34
par Ncdk » 21 Jan 2017, 13:34
Ah oui ! C'est
=\frac{1}{\Phi'(\Phi^{-1}(s))})
C'est vrai que c'est dans mes souvenirs lointain, je l'ai quasiment jamais utilisé

EDIT : Pour compléter, on a que
=f'(t)*\frac{1}{||f'(t)||})
et en passant à la norme on a bien
||=1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
en fonction de t.
