Bonjour à tous et bonne année 2008,
J'aimerais trouver la loi à appliquer dans le cadre dans cet exercice :
Exercice :
Si l'on suppose que les jours d'anniversaire sont répartis équitablement parmi les 365 jours de l'année et si l'on choisit 33 personnes au hasard dans l'annuaire, quelle est la probabilité pour qu'au moins deux de ces 33 personnes aient leur anniversaire le même jour ?
Je sais que la réponse à trouver est 0.77497185.
J'ai essayé la loi binomiale avec p(X >= 2) = 1 - ( p(X=0)+p(X=1)+p(X=2) ) mais je ne trouve pas le bon résultat.
J'ai mis ce sujet dans la partie "supérieure" car je suis en DUT.
Merci d'avance de vos réponses et meilleurs voeux.
[PROBA] Loi à déterminer.
4 messages
- Page 1 sur 1
Bonjour,
si l'on considère l'espace des probabilités comme étant celui des 33-uplets à valeurs dans les entiers de 1 à 365, il y a en tout cas possibles.
cas possibles.
P(au moins 2 sont nés...)=1-P(personne n'est né le même jour) or la probabilité pour qu'aucun ne soit né le même jour est correspond au nombre de 33-uplets constitué de nombres tous différents divisé par le nombre de cas possibles soit :
!}}{365^{33}}\simeq 0,22502814582422799763066977018833) et
et 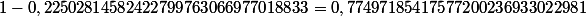 2
2
si l'on considère l'espace des probabilités comme étant celui des 33-uplets à valeurs dans les entiers de 1 à 365, il y a en tout
P(au moins 2 sont nés...)=1-P(personne n'est né le même jour) or la probabilité pour qu'aucun ne soit né le même jour est correspond au nombre de 33-uplets constitué de nombres tous différents divisé par le nombre de cas possibles soit :
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
