[Proba] Déterminer un paramètre d'une loi conjointe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 16 Oct 2014, 11:17
Bonjour,
j'ai besoin d'un peu d'aide concernant cet exercice :
Soit
)
un couple aléatoire à valeurs dans
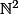
de loi définie par
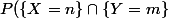=\dfrac{a}{(n+m+1)!})
.
Déterminer
.
Ma première idée consiste à exploiter le fait que
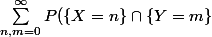 = 1)
.
Est-ce la bonne démarche ? Si oui, comment calculer cette somme (je ne suis pas très à l'aise avec les séries doubles) ?
Merci :we:
-
mathelot
par mathelot » 16 Oct 2014, 12:06
c'est normal que ça ne soit pas réduit dans (n+m+n)! ?
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 16 Oct 2014, 12:09
C'était une erreur de recopie merci, c'est corrigé !
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 16 Oct 2014, 12:19
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
par mathelot » 16 Oct 2014, 12:25
La somme vaut ae.
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 16 Oct 2014, 19:29
Ok c'est bon pour cette question :we:
On me demande ensuite :
Calculer la loi de
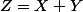
, d'identifier cette loi et de donner ses moments d'ordre 1 et 2.
En déduire l'espérance mathématique de
et
.
" Au feeling ", je dirais :
=\sum_{n=0}^k \dfrac{a}{(n+k-n+1)!}=\dfrac{e^{-1}}{k!})
c'est ça ?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 17 Oct 2014, 07:56
Oui :
=\sum_{n+m=k} p(X=n\text{ et }Y=m)=\sum_{n=0}^k p(X=n\text{ et }Y=k-n))
+1)!}=\frac{a}{k!}=\frac{e^{-1}}{k!})
Et c'est
une loi de Poisson de paramètre
.
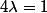
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
par