Limite d'une suite de matrices

[Zoulch]

Bonjour a tous,
J'ai une question :
On considère une suite de matrices telle que :




Je voudrais savoir si je peux écrire :

Pour tout ,

Merci d'avance !

[emdro]

Bonjour,

la réponse est OUI!

Quand dis-tu qu'une suite de matrice (Pn) tend vers Q ? Lorsque les coefficients de Pn tendent vers ceux de Q? Si c'est cela ta définition, c'est facile à démontrer.

[Zoulch]

Voila pour la convergence

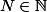
On dit qu'une suite de matrice converge vers une matrice si et seulement si pour tout , il existe tel que si , alors ...

la norme doit etre la norme subordonnee?

Quand tu dis que ca marche, le resultat vient d'ou (je pensais a la limite du produit qui serait le produit des limites...mais ca ne marche surement pas pour matrice et vecteur?)

[emdro]

Si tu as le résultat concernant le produit dans ton cours, pourquoi ne pas considérer un vecteur comme une matrice n*1? :happy2:

[Zoulch]

He non je n'ai pas ce fameux résultat (a part pour des suites de reels, mais c'est pas le cas)...

Merci qd même...

[emdro]

En dimension finie, toutes les normes sont équivalentes. Tu peux prendre celle que tu souhaites.

Par exemple avec .

En notant et et en supposant que:
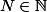
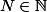
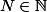
pour tout , il existe tel que si , alors , il existe tel que si , alors, il existe tel que si , alors

Ce qui prouve bien que tend vers , non?

[Zoulch]

Quand tu mets

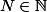
pour tout , il existe tel que si , alors

tu utilise le fait que ? (norme matricielle est sous-multiplicative?)

Sinon pour ta demo, merci je suis arrive a un truc semblable, c'est bien un raisonnement classique sur les limites

Merci bcp !

[emdro]

tu utilise le fait que ? (norme matricielle est sous-multiplicative?)

A aucun moment!

J'ai écrit que .

A la prochaine. :we: