Limite d'une série presque géométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 02 Oct 2012, 15:23
par Wenneguen » 02 Oct 2012, 15:23
Bonjour,
je dois montrer que
^2} = \sum_{n=0}^{+\infty} (n+1)a^n)
, mais je sais pas comment m'y prendre, un petit indice ? :we:
Merci !
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Oct 2012, 15:26
par Judoboy » 02 Oct 2012, 15:26
J'ai bien l'impression de voir une dérivée d'un truc connu.
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 02 Oct 2012, 16:01
par Wenneguen » 02 Oct 2012, 16:01
Je ne vois pas...
-
SimonB
 par SimonB » 02 Oct 2012, 16:43
par SimonB » 02 Oct 2012, 16:43
De quoi le machin à gauche est-il la dérivée ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Oct 2012, 16:50
par Doraki » 02 Oct 2012, 16:50
multiplie la somme par 1-a, simplifie, remultiplie par 1-a, resimplifie, et voilà.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 02 Oct 2012, 17:29
par Luc » 02 Oct 2012, 17:29
Wenneguen a écrit:Bonjour,
je dois montrer que
^2} = \sum_{n=0}^{+\infty} (n+1)a^n)
, mais je sais pas comment m'y prendre, un petit indice ? :we:
Merci !
Bonjour,
si tu regardes l'identité des séries formelles, c'est immédiat par dérivation de
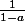
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 02 Oct 2012, 17:34
par Wenneguen » 02 Oct 2012, 17:34
Luc a écrit:Bonjour,
si tu regardes l'identité des séries formelles, c'est immédiat par dérivation de
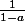
L'identité des séries formelles ? ^^
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 02 Oct 2012, 18:06
par Luc » 02 Oct 2012, 18:06
Wenneguen a écrit:L'identité des séries formelles ? ^^
C'est juste dire que tu ne te préoccupe pas des problèmes de convergence, et que tu dérives avec les règles de calcul habituelles.
-
Anonyme
 par Anonyme » 02 Oct 2012, 20:19
par Anonyme » 02 Oct 2012, 20:19
Le mot magique est : une série entière
Que connais tu sur la série la série
= \sum_{k=0}^{N} x^k)
avec

un réel donné ?
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 02 Oct 2012, 20:25
par Wenneguen » 02 Oct 2012, 20:25
ptitnoir a écrit:Le mot magique est : une série entière
Que connais tu sur la série la série
= \sum_{k=0}^{N} x^k)
avec

un réel donné ?
Elle converge vers
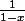
si
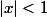
et diverge sinon ?
-
Anonyme
 par Anonyme » 02 Oct 2012, 20:46
par Anonyme » 02 Oct 2012, 20:46
OUI et voici d'autres questions
1) quand cette série converge, peux tu calculer la limite de S_N(x) quand N tend vers +infini (qu'on peut noter
)
)
2) Quelles sont les conditions pour qu'une série entière soit dérivable termes à termes
c'est à dire que
= \sum_{k=1}^{+\infty} kx^{k-1}=\sum_{k=0}^{+\infty} (k+1)x^{k})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités