Limite d'un produit de deux suites

[AceVentura]

Bonjour,
j'ai un gros doute sur la démonstration d'une propriété : montrer que si deux suites réelles et converge respectivement vers et , alors le produit des suites converge vers .

Alors :



Puis, pour , on a :



La suite converge, donc elle bornée : il existe (ici je fais le premier blocage, car pourquoi M serait forcément strictement positif ?) tel que .

Donc (et voici le second blocage, pourquoi :hein:)


Merci encore !

[Doraki]

Puisque Un est bornée, il existe a et b tel que pour tout n, a < un < b.
Si M = max(|a|,|b|), alors -M <= a <= un <= b <= M.
Comme une valeur absolue est positive, bah M sera positif.
Et M peut pas être nul car ça voudrait dire que a=b=0, et que 0 < un < 0.

En outre, si jamais un jour tu trouves un M négatif et un x tel que |x| < M <= 0,
bah t'auras trouvé un x dont la valeur absolue est négative. Donc ça risque pas d'arriver.

Pour ton blocage 1-et-demi-que-t'as-pas-repéré, c'est que apparemment y'a 3 epsilons différents dans la preuve.
Y'a le "soit epsilon positif, montrons qu'il existe N tel que |un*vn - l1*l2| <= epsilon pour n >= N".
Et puis y'a les "un converge vers l1 donc il existe N1 tel que |un - l1|<= e pour n >= N1", sauf que là, e on l'a choisi qui vaut epsilon/2M.
Et pareil pour l'autre suite, où on a choisi epsilon/2|l1|.

Enfin, pour ton 2ème blocage, évidemment si l1 est nul c'est un peu gênant,
donc on regarde un peu mieux ce qui se passe dans ce cas et on s'aperçoit que le morceau de droite, en fait il vaut déjà 0, donc on a même pas besoin de savoir que la suite vn converge, on utilise juste le fait qu'elle est bornée pour avoir le M dans le morceau de gauche.

[AlexisD]

Bonjour,

Pour ta démonstration, il est en effet judicieux d'utiliser le fait que la suite (Vn) était bornée, d'où l'existence de ton M
Mais je te conseille de considérer deux cas:

Le premier est de supposer que M est égal à 0. Cela voudrait dire qu'à partir d'un certain rang, tous les termes de la suite sont nuls. Il est alors immédiat de montrer que la suite UnVn converge (immédiat: pourquoi ?)

Dans le second cas, tu n'es plus embêté.


Concernant ta deuxième égalité, je ne comprends pas tous tes quotients. Apparemment tu as cherché quel dans chacune des hypothèses. Mais si on garde le tout tel quel, on obtient:


Donc il s'agit de prendre effectivement:

Et la, tu as raison de te poser la question de la non nullité de l_1, en effet. Mais il faut raisonner comme avec M et éliminer le cas douteux où .

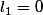
Voilà, j"espère avoir répondu à ta question...