Limite de fonction à plusieurs variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rhaegar
- Membre Naturel
- Messages: 91
- Enregistré le: 25 Mar 2017, 21:27
-
 par Rhaegar » 30 Oct 2017, 12:55
par Rhaegar » 30 Oct 2017, 12:55
Bonjour,
Je sais ne sais pas comment faire dans l'exercice suivant :
Etudier la limite suivante :
\to (0,0)} \frac{xy}{x+y})
La limite semble être 0 mais je ne vois pas comment le montrer. Je ne connais pas la méthode générale.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 30 Oct 2017, 13:12
par Lostounet » 30 Oct 2017, 13:12
Salut,
Pour moi cette limite n'existe pas (elle ne vaut pas 0). Pour le voir j'ai pris des suites (xn) et (yn) telles que (xn;yn) tend vers (0;0).
J'ai regardé f(xn;yn) pour voir la limite obtenue. Par exemple si tu prends xn=1/n et yn=-1/(n+1)
Alors f(xn;yn)=-1/(n^2+n):(1/(n(n+1))
De limite -1 ..!
En fait je ne prends pas les suites au hasard: f n'est pas définie en x=-y. Donc je prends xn et yn des suites "proches de ce problème".
Sauf erreur de ma part...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 30 Oct 2017, 13:17
par Viko » 30 Oct 2017, 13:17
f n'est pas définie en y=-x tu veux dire ?
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 30 Oct 2017, 13:18
par Lostounet » 30 Oct 2017, 13:18
Oui.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Rhaegar
- Membre Naturel
- Messages: 91
- Enregistré le: 25 Mar 2017, 21:27
-
 par Rhaegar » 30 Oct 2017, 13:37
par Rhaegar » 30 Oct 2017, 13:37
Donc si je veux montrer que la limite n'existe pas, je dois prendre deux suites (xn, yn) et (x'n, y'n) convergent vers (0,0) et montrer que lim(f(xn,yn)) != lim(f(x'n,y'n)).
Par exemple ici, (xn, yn) la suite que tu as dit et (x'n,y'n) =(1/n, 1/n).
Je ne comprends pas ce que tu dis quand tu dis que tu prends une suite "proche du problème". Je ne vois pas comment tu as trouvés les suites en voyant que y=-x.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 30 Oct 2017, 13:46
par Viko » 30 Oct 2017, 13:46
le problème ici est la valeur interdite donc quand il dit qu'il prend des suites "proche du problème" il entend qu'il prend des suites proche de cette valeur interdite en effet quand n est grand
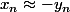
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
Rhaegar
- Membre Naturel
- Messages: 91
- Enregistré le: 25 Mar 2017, 21:27
-
 par Rhaegar » 30 Oct 2017, 14:11
par Rhaegar » 30 Oct 2017, 14:11
ok merci


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Oct 2017, 15:15
par chan79 » 30 Oct 2017, 15:15
salut
On peut essayer de chercher la limite de f(x,y) avec la condition y=-x/(x+1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités