Lignes de niveau
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
hervedo
- Membre Naturel
- Messages: 52
- Enregistré le: 09 Déc 2007, 16:19
-
 par hervedo » 24 Mar 2008, 21:46
par hervedo » 24 Mar 2008, 21:46
Bonsoir à tous,
J ai un problème sur les fonctions à deux variables...Soit f(x,y)=
.e^{y-x^2})
1. Déterminer les points critiques de f...je trouve que tous les points de coordonnées (x,x^2-1) sont des points critiques
2. Etudier la fonction g tq g(t)=t.e^t et en déduire la nature des points critiques. J ai montré que pour tout t g(t)>=-1/e donc -1/e est min global sur IR^2 atteint pour tout point de coordonnées (x,x^2-1)
3. Discuter en fonction de k la nature de C_k={...f(x,y)=k} et là je bloque !!
Merci par avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Mar 2008, 22:57
par yos » 24 Mar 2008, 22:57
f(x,y)=g(t) pour t=...
Donc :
si k<-1/e, C_k est l'ensemble vide,
si k=-1/e, C_k est la parabole y=x²-1.
si k>-1/e, C_k est réunion des paraboles y=x²+a et y=x²+b où a et b sont les antécédents de k par g.
-
hervedo
- Membre Naturel
- Messages: 52
- Enregistré le: 09 Déc 2007, 16:19
-
 par hervedo » 26 Mar 2008, 10:35
par hervedo » 26 Mar 2008, 10:35
Merci c est ce que j ai trouvé aussi.
D ailleurs je crois qu en fait si -1/e0 il n y a qu une seule parabole.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Mar 2008, 13:55
par yos » 26 Mar 2008, 13:55
Oui j'avais pas les variations de g en tête : un seul antécédent pour
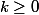
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
