Ligne de niveau/ barycentre

[ThekamikazeFou]

Bonjour, après avoir corrigé un exercice de cours, il y a une résultat que je ne comprends pas.

j'ai un triange rectangle ABC rectangle en A ou [AB] = 4a; [AC] = 2a et I est le millieu de [AB]

j'ai une fonction : g(M) = (MA + MB -2 MC).(-MA+2MB) tout cela en vecteur.

on me demande donc de calculer G(A) en fonction de a.

j'ai donc fait ceci :
g(A) = (AB -2AC).2AB tout cela en vecteur

et je suis censé trouver g(A) = 32a²

mais je ne comprends pas comment faire.

je dois calculer g(A)² pour pouvoir avoir les longueurs? merci !

Edit :
le problème c'est que je ne comprendre pas AB - 2AC car si je met cela au carré c'est égale à 0

[wserdx]

Revois ton calcul. Si M est un point variable, il ne doit pas apparaître dans l'expression g(A).
Tu devrais trouver car

[ThekamikazeFou]

Revois ton calcul. Si M est un point variable, il ne doit pas apparaître dans l'expression g(A).
Tu devrais trouver car

Faute de frappe dsl c'est modifié!

Mais je ne comprends pas comment tu passe d'une expression a l'autre ici :



La géometrie est vraiment mon point faible, pourtant ce n'est pas faute de travailler, je melange tout avec les vecteurs :/

[Anonyme]

@ThekamikazeFou

Les vecteurs ce n'est pas compliqué si tu as compris que

1)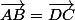 si et seulement si 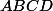est un parallélogramme (éventuellement "plat")

2) que la translation d'un point par un vecteur est une transformation du plan et donne un point B tel que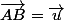
et on note

3) qu'une droite qui passe par le point et de vecteur directeur 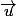est l'ensemble des points
tels que les 2 vecteurs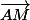 et sont colinéaires
- soit faire le produit croisé des coordonnées (ou le déterminant de ces 2 vecteurs) et vérifier qu'il est nul
- soit montrer qu'il existe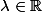 tel que

4) si le point est le milieu du segment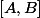
alors on a :
- soit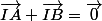
- soit

ET
quand tu as compris ces 4 notions : Il faut connaitre / retenir

1) la loi (interne) d'addition de 2 vecteurs (et la loi de Chasles) , très facile à comprendre en faisant un dessin...

2) la loi : produit scalaire de 2 vecteurs qui donne comme résultat un nombre
et la notion d'orthogonalité de 2 vecteurs....