Lemme de Fatou
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Martin Gale
- Messages: 3
- Enregistré le: 06 Nov 2012, 01:03
-
 par Martin Gale » 06 Nov 2012, 01:09
par Martin Gale » 06 Nov 2012, 01:09
Bonjour à tous, je viens de voir le lemme de fatou en cours, et il y a certaines notions basiques qui méchappent un peu

en fait, j'ai du mal à comprendre ce que signifie l'intégrale de la limite d'une fonction.. et en quoi cela est il différent de la limite de l'intégrale.
Voilà, merci d'avance pour vos réponses
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 06 Nov 2012, 12:11
par arnaud32 » 06 Nov 2012, 12:11
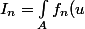du)
est une suite de reels

definie pour tout x par
=\lim_{n\rightarrow \infty}f_n(x))
(limite simple)
tu n'as pas a priori
du= \lim_{n \rightarrow \infty}I_n)
-
Martin Gale
- Messages: 3
- Enregistré le: 06 Nov 2012, 01:03
-
 par Martin Gale » 06 Nov 2012, 21:57
par Martin Gale » 06 Nov 2012, 21:57
arnaud32 a écrit: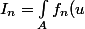du)
est une suite de reels

definie pour tout x par
=\lim_{n\rightarrow \infty}f_n(x))
(limite simple)
tu n'as pas a priori
du= \lim_{n \rightarrow \infty}I_n)
merci de ta réactivité arnaud, mais ma question portait plus sur ce à quoi correspondait l'intégrale d'une limite, s'agit il de l'air se trouvant sous la fonction jusqu'à +infini, dans ce cas là, c'est la meme chose que la limite de l'intégrale si je ne me trompe.. or le lemme de fatou dit cette dernière est supérieure ou égale à l'autre
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 07 Nov 2012, 10:12
par arnaud32 » 07 Nov 2012, 10:12
pour faire simple:
 = x^n)
sur [0,1]
la fonction limite f est definie (si elle existe) par
= \lim_{n \rightarrow \infty} f_n(x) = \lim_{n \rightarrow \infty} x^n)
pour

,
 = 0)
et f(1)=1
(tu remarques au passage que la fonction limite f n'est pas continue
(u)du = \int_0^1 f(u)du)
-
Martin Gale
- Messages: 3
- Enregistré le: 06 Nov 2012, 01:03
-
 par Martin Gale » 08 Nov 2012, 00:16
par Martin Gale » 08 Nov 2012, 00:16
merci de ton aide, c'est beaucoup plus claire maintenant!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
est une suite de reels
definie pour tout x par
(limite simple)