(R,*) isomorphe a (R,+)

par **HanZel** » 29 Oct 2008, 20:42

Bonjour,
J'ai une Loi de composition interne: * et je dois montrer que (R,*) est un groupe isomorphe a (R,+).
Lorsqu'il s'agit de prouver qu'une fonction est un isomorphisme, je n'est aucun problème, mais la je ne sais pas comment faire sans l'aide d'une fonction... :triste:
Pour prouver que (R,*) est un groupe, je n'ai pas de problème, mais pourriez vous m'indiquez la marche a suivre pour montrer que (R,*) est isomorphe a (R,+) : injection, surjection, noyau, image?....
Je ne vous met pas x*y=.... pour éviter que la réponse ne me tombe directement dans le bec, mais si c'est nécessaire je vous la donnerai.
Merci :happy2:

par **leon1789** » 29 Oct 2008, 20:47

Connais-tu une fonction f telle que f(x+y)=f(x).f(y) ou si tu préfères f(xy)=f(x)+f(y) ?

par **HanZel** » 29 Oct 2008, 20:50

avec la loi de multiplication, je connais le log et l'exponentielle, mais pas avec la loi "étoile"
Alors en fait il faudrait que je trouve une fonction telle que f(x*y)=f(x)+f(y) ?
sachant que * est une loi "etoile" pas multiplicative.

par **abcd22** » 29 Oct 2008, 20:56

HanZel a écrit:Alors en fait il faudrait que je trouve une fonction telle que f(x*y)=f(x)+f(y) ?
sachant que * est une loi "etoile" pas multiplicative.

Oui, il faut¹ trouver un morphisme de groupes de (R, *) dans (R, +) (ou de (R, +) dans (R, *), au choix) qui est un isomorphisme.

¹enfin, il suffit plutôt.

par **HanZel** » 29 Oct 2008, 21:05

D'accord, je vais cherché ça et je vous demanderez quand même confirmation après :happy2:
Merci à vous ! :lol4:

par **leon1789** » 29 Oct 2008, 21:06

HanZel a écrit:avec la loi de multiplication, je connais le log et l'exponentielle, mais pas avec la loi "étoile"
Alors en fait il faudrait que je trouve une fonction telle que f(x*y)=f(x)+f(y) ?
sachant que * est une loi "etoile" pas multiplicative.

désolé, j'ai lu trop vite en croyant que * était la multiplication... ce qui est complètement idiot puisque (R, multiplication) n'est pas un groupe (à cause de 0)

par **Doraki** » 29 Oct 2008, 21:06

euh (R,*) c'est pas un groupe.

A moins que "*" soit autre chose que la multiplication et dans ce cas là personne ne sait de quoi tu parles.

par **leon1789** » 29 Oct 2008, 21:07

Doraki a écrit:euh (R,*) c'est pas un groupe.

tu as lu trop vite, comme moi ! * est une loi interne qui n'est pas la multiplication. :id:

par **HanZel** » 29 Oct 2008, 21:10

Heuu, si mon (R,*) a : associativité, élément neutre et symétrique (+commutatif) pour tout x de R et est différent de l'ensemble vide donc a priori c'est un groupe, non?

[EDIT] Oui "*" est autre chose que la multiplication.
j'aurais du mettre un autre symbole mais j'ai pas trouvé ^^
Et je voulais savoir la manière de procéder pour montrer qu'il est isomorphe a (R,+) et je pense avoir eu ma réponse, s'il suffit de trouver une fonction qui marche si je peux dire ca comme ca.

par **leon1789** » 29 Oct 2008, 21:28

De toute manière il est fort probable qu'il te faille trouver une bijection f telle que f(x*y) = f(x)+f(y) et/ou sa réciproque...

par **HanZel** » 29 Oct 2008, 22:58

Je crois que j'ai fait beaucoup de vent pour pas grand chose, mais pour moi ça valait le coup, voyons quand même si ce que j'ai fait est bon.
Alors voila, j'ai ma LCI * qui est :

Donc j'ai prouvé que

était un groupe.
On a :
- élément neutre e: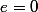

- symétrique de x :

Puis j'ai pris une fonction

tel que :

Ensuite :

= {

} (le noyau est l'ensemble des

de

tel que

soit

)

Le noyau est réduit à l'élément neutre donc

est injective.

= {

;)

,

;)

:

} (l'image est l'ensemble des

de

tel qu'il existe

de

ayant pour image par

:

)
Soit

;)

. S'il existe

;)

tel que

, alors

, or

existe puisque

;)

donc il existe bien

tel que

.
Donc

est surjective.

est injective et surjective donc

est bijective, ainsi on peut en conclure que

est un groupe isomorphe a

.

Voila ce que j'ai fait.

Pourriez vous me dire les erreurs que j'ai faites autant dans le raisonnement que dans la rédaction, en particulier je ne suis pas sur de moi en ce qui concerne l'image

Merci :happy2:

PS: si le noyau est réduit à l'élément neutre, cela implique-t-il que le x de y=f(x) est unique lors de la surjection?

par **leon1789** » 29 Oct 2008, 23:12

HanZel a écrit:Je crois que j'ai fait beaucoup de vent pour pas grand chose, mais pour moi ça valait le coup,

...et c'est bien ça le principal ! :id: Le forum existe pour ça.

HanZel a écrit:(...)
est injective et surjective donc est bijective, ainsi on peut en conclure que est un groupe isomorphe a .

Voila ce que j'ai fait.

c'est ok.

--------------
Juste des remarques sur la rédaction :

HanZel a écrit:Puis j'ai pris une fonction tel que :

pourquoi "une" ? il n'y a qu'une fonction comme celle-là : c'est LA fonction x -> x^5.

HanZel a écrit:est injective et surjective donc est bijective,

Pour la bijectivité de f, je trouve ta preuve un peu lourde : x -> x^5 est bijective, son application réciproque est x -> x^(1/5), non ?

--------------

HanZel a écrit:PS: si le noyau est réduit à l'élément neutre, cela implique-t-il que le x de y=f(x) est unique lors de la surjection?

ha oui, c'est fait pour ça !

par **HanZel** » 29 Oct 2008, 23:40

Pour la bijectivité de f, je trouve ta preuve un peu lourde : x -> x^5 est bijective, son application réciproque est x -> x^(1/5), non ?

Me suffit-il de dire que si j'ai f(x)=x^5 (f donnée) et g(x)=x^(1/5) (g, bien choisie) et que (fog)(x)=id alors je peux conclure que f est bijective avec f-1=g?

PS: si le noyau est réduit à l'élément neutre, cela implique-t-il que le x de y=f(x) est unique lors de la surjection?
ha oui, c'est fait pour ça !

Si le noyau n'est pas réduit à l'élément neutre, cela implique-t-il qu'il existe plusieurs x tel que y=f(x) ou qu'il n'y existe pas x pour un certain y ou les deux ou soit l'un soit l'autre ou pas forcément, l'application peut quand même être bijective?
Je suis assez alaise dans l'algebre linéaire et les applications linéaires (je suis en L2 maths), mais je dois dire que pour les groupes et tout, je trouve que c'est assez ... vaste^^

Un grand merci léon pour m'avoir corrigé et à tous de pour m'avoir guider :ptdr:

par **ThSQ** » 30 Oct 2008, 08:04

Exo assez artificiel car pour toute bijection f entre deux ensembles

permet de "transférer" une structure de groupe d'un ensemble à un autre.

par **HanZel** » 30 Oct 2008, 12:16

ThSQ a écrit:Exo assez artificiel car pour toute bijection f entre deux ensembles permet de "transférer" une structure de groupe d'un ensemble à un autre.

Oui c'est vrai, assez artificiel, mais quand tu commences à apprendre ça fait pas de mal :ptdr:

HanZel a écrit:Si le noyau n'est pas réduit à l'élément neutre, cela implique-t-il qu'il existe plusieurs x tel que y=f(x) ou qu'il n'y existe pas x pour un certain y ou les deux ou soit l'un soit l'autre ou pas forcément, l'application peut quand même être bijective?

Quelqu'un pourrait-t-il m'éclairer a se sujet?

par **Doraki** » 30 Oct 2008, 13:02

Ker f = 0
<=> pour tout x, f(x)=0 => x=0
<=> pour tout x,y, f(x-y)=0 => x-y=0
<=> pour tout x,y, f(x)-f(y)=0 => x-y=0
<=> pour tout x,y, f(x)=f(y) => x=y
<=> f est injective

(R,*) isomorphe a (R,+)

(R,*) isomorphe a (R,+)

Qui est en ligne