Isomorphe

[zork]

Bonjour,

soit f:A-->B un morphisme entre anneaux commutatif. Montrer que A/kerf est isomorphe à f(A)


Je n'ai aucune idée de comment partir. Pouvez vous m'aider?



merci

[arnaud32]

que veux dire isomorphe?
quelle est la structure de f(A), de A/Ker(f) ?
peux tu trouver un morphisme simple de A/Ker(f) dans f(A)? est il injectif? surjectif?

[zork]

il existe un morphisme f d'anneau bijectif. et f(0)=0 f(1)=1

en faites je ne vois pas ce qu'est A/kerf

[arnaud32]

tu notes C(x) la classe de x selon f, qui est {y€A | f(y)=f(x)}
A/Ker(f) = { C(x)| x€A}

est ce que f(A) est un anneau?
estce que A/Ker(f) est un anneau?
que penses tu de gqui va de A/Ker(f) dasn f(A) telle que g( C(x) ) = f(x) ?

[zork]

mais ici a-t-on besoin de connaitre A/kerf ou on peut trouver directement l'isomorphisme sans savoir ce qu'est A/kerf?

[arnaud32]

mais ici a-t-on besoin de connaitre A/kerf ou on peut trouver directement l'isomorphisme sans savoir ce qu'est A/kerf?

tu veux montrer que A/Ker(f) est isomorphe a f(A) ok mais pour quelle structure?
tu dois donc bien connaitre la nature de ces deux ensembles
pour l'isomorphisme, il decoule assez directement de f

[zork]

je ne vois toujours pas quels sont les éléments de A/kerf

par exemple, Z/2Z={0,1} mais ici A/kerf je ne le sais pas.

D'autre part pour déterminer un isomorphisme, en TD on utilisait le fait que f(1)=1. Par exemple les isomorphisme de (Z,+,.).
Mais ici cette technique ne marche pas

[alm]

Salut
Je crois qu'il faut que tu consulte ton cours pour ce qui est des lois de
En général, si est un anneau commutatif et si est un idéal de alors si on note la classe d'équivalence de 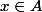modulo alors si et sont dans on défini : et .
Ton cours contient en principe la justification de ces définition à savoir la compatibilité des lois de avec la relation d'équivalence associée à l'idéal : Autrement dit : si on remplace par d'autres représentants des classes , le résultat ne change pas

[alm]

A/kerf je ne le sais pas.

Les élèments de sont lorsque décrit

Justement si et tel que alors



Apparement ça donne une infinité d'éléments à savoir:




Mais en réalité il n y a que deux éléments car chacun des éléments ci-dessus est égal soit à soit à suivant que est pair ou impair .

[zork]

je suppose qu'il existe un isomorphisme g de A/kerf-->f(A)

x* dans A/kerf, g(x*)=g(x+kerf)=g(x)+g(kerf)=g(x)+g(0)=g(x)

mais quelle est la forme de g(x). avec g(x) dans f(A)?

[alm]

je suppose qu'il existe un isomorphisme g de A/kerf-->f(A)

x* dans A/kerf, g(x*)=g(x+kerf)=g(x)+g(kerf)=g(x)+g(0)=g(x)

mais quelle est la forme de g(x). avec g(x) dans f(A)?

tu t'approches de la bonne réponse

Je t'aide un peu :

Pour x* dans A/ ker f tu pose g(x*)=f(x)

Le problème est de justifier d'abord que g est bien définie : autrement dit si x*=y* alors f(x)=f(y) ...essaye de voir pourquoi (c'est simple)

Ensuite que c'est un morphisme g(x* + y ) g(x*) + g(y*) et g(x*y*)=g(x*) g(y*) pour tout x* et y* de A/ker f

Finalement que g est bijective : injective g(x*)=g(y*) implique x*=y* pour tout x*,y* de A/ ker f
g surjective si Y est un élément de f(A) exhibe un antécédant de Y par g (indic : il existe x de A tel que f(x)=Y ...)

[zork]

d'accord merci