Bonjour à tous
J'aurais besoin d'un petit coup de main concernant une démonstration que je ne comprends pas. Voici l'énoncé:
Soit G un groupe non abélien d'ordre 12. Soit H un 3-Sylow de G. On considère le morphisme
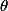
: G ->

correspondant à l'action de G par translation sur G/H. Montrer que ce morphisme n'est pas injectif si et seulement si H est distingué dans G. En déduire que si H n'est pas distingué dans G, le groupe G est isomorphe à A4.
Et voici la résolution :
On a
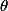
(g)(xH)=gxH (g et x dans G). Le noyau de
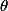
est l'intersection de tous les conjugués de

de H
(ça déjà je comprends pas trop... Pour g dans le noyau, on a theta(g)(xH)=xH, c'est bien ça ? Comment on en déduit cette histoire de conjugués ?). C'est-à-dire, d'après les théorèmes de Sylow, l'intersection de tous les 3-Sylow de G
(ok, parce que tous les 3-Sylow sont conjugués, et j'imagine qu'il n'y a rien d'autre dans la classe de conjugaison). Comme l'intersection de deux 3-Sylow est triviale, le noyau est différent de {1} ssi il n'existe qu'un seul 3-Sylow, qui est alors distingué
(Ok, ça c'est l'un des théoème de Sylow). Si H est non distingué dans G, alors
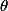
est injectif
(ok, par ce qu'on vient de démontrer) et fournit un isomorphisme entre G et un sous groupe de S4
(ça par contre je vois pas du tout... il induit un isomorphisme entre G et son image, puisqu'il est injectif, mais comment en déduit-on ce sous-groupe de S4 ?!). Ce groupe devant être d'odre 12 comme G
(pourquoi ?!), c'est nécessairement A4.
Voilà, mes questions sont dans le texte de résolution. J'ai dû m'intéresser aux théorèmes de Sylow dans le cadre de ce théorème, mais je ne suis pas du tout familière avec ces notions. Est-ce que ce que je ne comprends pas vient de théorèmes que j'ignore ? Est-ce qu'une explication simple m'a échappée ?
Merci d'avance de votre précieuse aide !
