L'inverse d'une homographie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
WhiteShadow
- Membre Naturel
- Messages: 63
- Enregistré le: 09 Aoû 2013, 14:06
-
 par WhiteShadow » 04 Sep 2013, 11:16
par WhiteShadow » 04 Sep 2013, 11:16
Bonjour,
J'ai une homographie

telle que:
=\frac{az + b}{cz + d})
où

et

Je sais que l'inverse de cette application est également une homographie. Mais je ne parviens pas à trouver sa formule (certainement dû à la fatigue) et je n'ai rien vu sur le net. Est-ce que quelqu'un peut me donner la solution?
Merci d'avance
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 04 Sep 2013, 11:38
par adrien69 » 04 Sep 2013, 11:38
Yop,
T'as une matrice
)
de déterminant 1.
C'est quoi son inverse ?
-
WhiteShadow
- Membre Naturel
- Messages: 63
- Enregistré le: 09 Aoû 2013, 14:06
-
 par WhiteShadow » 04 Sep 2013, 11:41
par WhiteShadow » 04 Sep 2013, 11:41
C'est ça qu'on appelle un moment de solitude?? :doh:
Merci Adrien... :ptdr:
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 04 Sep 2013, 11:58
par adrien69 » 04 Sep 2013, 11:58
Je t'en prie ;)
(faut juste pas oublier que les homographies c'est exactement les matrices en fait)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 04 Sep 2013, 12:13
par Doraki » 04 Sep 2013, 12:13
Presque, les homographies c'est isomorphe à PSL2(R).
La matrice -I2 et la matrice I2 correspondent à la même homographie.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Sep 2013, 12:13
par lapras » 04 Sep 2013, 12:13
adrien69 a écrit:Je t'en prie

(faut juste pas oublier que les homographies c'est exactement les matrices en fait)
Pour compléter ta réponse, il y a une manière conceptuelle pour l'existence du morphisme GL2(R) -> homographie (dont le noyau = +/- I_2), ou autrement dit pourquoi composer deux homographies revient à composer les matrices associées.
Simplement tu peux faire agir GL2(R) sur l'espace projectif P^1(R) (=ensemble des droites de R^2) car GL2(R) agit sur les droites de R^2. Et si tu regardes les coordonnées homogènes (x:y) sur P^1(R) ( (x:y) représente la droite de vecteur directeur (x,y)), alors une matrice g=(a b ; c d) va agir par g.(x:y) = (ax+by:cx+dy)=((ax+by)/(cx+dy) : 1) car on travaille en coordonnées homogènes. Autrement dit via l'identification de R comme un sous ensemble (ouvert) de P^1(R) ( par t -> (t:1) ), GL2(R) agit par homographies sur R.
Pour résumer : une homographie c'est juste une transformation linéaire mais dans l'espace projectif. Ca permet de comprendre géométriquement ces transformations. En fait le morphisme expliqué avec R marche pour tout corps, car ce que j'ai dit est purement algébrique. Et j'ajoute que l'espace projectif permet de traiter le point à l'infini (quand ct+d=0) comme un point comme les autres (de coordonnées (0:1)).
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 04 Sep 2013, 12:26
par adrien69 » 04 Sep 2013, 12:26
Tout ce que je voulais dire c'est que ça marche tout pareil vous savez, pas la peine de sortir les gros sabots (ni le Lang d'ailleurs)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Sep 2013, 12:43
par lapras » 04 Sep 2013, 12:43
Oui bien sur ce n'est pas nécessaire, mais je l'ai ajouté car je pense qu'on ne comprends vraiment ce morphisme que si on le voit par l'espace projectif. Et souvent on le prouve par un calcul direct peu éclairant.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 04 Sep 2013, 14:53
par deltab » 04 Sep 2013, 14:53
WhiteShadow a écrit:Bonjour,
J'ai une homographie

telle que:
=\frac{az + b}{cz + d})
où

et

Je sais que l'inverse de cette application est également une homographie. Mais je ne parviens pas à trouver sa formule (certainement dû à la fatigue) et je n'ai rien vu sur le net. Est-ce que quelqu'un peut me donner la solution?
Merci d'avance
Il suffit de résoudre l'équation en

,

, on trouve alors

, l'inverse de l'homographie

est l'homographie

avec

et l'on a:
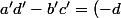(-a)-bc=1)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
