Intersection d'un compact et d'un fermé

[chombier]

J'ai une question sur le El Hage Hassan page 121. J'y lis ceci :



Voici ma question : pour le point 1, je pense qu'il n'est pas nécessaire que X soit séparé.

On utilise le résultat suivant de la même page :



Voici ma preuve du point 1 (où X n'est pas séparé) :

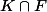
Proposition : Soit un espace topologique quelconque. Si K est une partie compact de X et F une partie fermée de X alors est un compact de X

est un compact muni de la topologie induite par celle de (X, T)

F est un fermé de X donc est un fermé de (K, T_K).
est un espace compact et est un fermé de donc d'après le théorème 3.1.1 est un compact de (K, T_K).
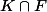
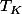
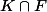
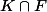
est un compact pour la topologie induite par , où est la topologie induite par sur K. Mais la topologie sur induite par et la topologie induite sur par coincident (ce qu'un auteur appelle la transitivité de la topologie induite).
Donc est un compact de (X, T_X).

Qu'en pensez-vous ? X doit-il être séparé ou non ?

[chombier]

J'essaie de montrer le point 3 du même corollaire :

Corollaire 3.1.1. Soit X un espace topologique séparé.
Si est une famille de parties compactes de X alors est un compact de X.

Si , K n'est pas vraiment défini. Je pense qu'il faudrait spécifier que la famille doit être non vide.

Si :
Tout d'abord, X est séparé donc K est séparé.
Pour tout , est un compact de X et X est séparé donc est fermé.
Tout les sont fermés donc K est fermé (l'ensemble des fermés est stable par intersection quelconque)
Soit quelconque. K est un fermé de et est un compact donc K est un compact.

[chombier]

Je m'attaque maintenant au point 2. L'équivalence me gène car dans un sens on n'utilise pas toutes les hypothèses. Je vais donc séparer les deux équivalences (d'autant qu'en vérité une seule des deux est vraiment interessante à mon avis).

Soit un espace topologique quelconque et une famille de fermés de X. On pose . Si F est un compact alors tous les sont des compacts.

Preuve : Soit .
est un fermé de X, et F est un compact donc d'après le théorème 3.1.1, F_i est un compact.

Soit un espace topologique séparé et une famille de compacts de X. On pose . Alors K est un compact.

Soit un recouvrement d'ouvers de K.
Autrement dit et .

Soit . La famille recouvre K donc elle recouvre K_i.
Or K_i est un compact donc il existe une sous-famille finie J_i de I telle que recouvre K_i.

L'union des J_i est une union finie d'ensemble fini donc avec est un recouvrement fini de K. Donc K est un quasi-compact.

X est séparé donc K est séparé, donc K est un compact.