Intégrales multiples et produits de fonctions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
friz
- Messages: 2
- Enregistré le: 21 Juin 2012, 15:44
-
par friz » 21 Juin 2012, 16:07
Bonjour à tous,
Je suis confronté à un problème. J'aurais besoin de déterminer si l'égalité A=B est correcte ou non pour un problème de physique. Voici les expressions de A et B.
 \int_x^e f(y) g(y) dy dx)
 g(x) \int_0^x f(y) dy dx)
Les fonctions f et g sont positives.
N'arrivant pas à établir analytiquement cette égalité, j'ai essayé d'intégrer numériquement A puis B (en essayant plusieurs types de fonctions : polynomiales, trigonométriques...). A prime abord, il semblerait que l'égalité soit vérifiée.
Maintenant, j'aimerais savoir si c'est vraiment le cas. Et si oui, comment peut on passer de l'expression de A à celle de B.
Merci d'avance pour votre aide.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 22 Juin 2012, 17:23
Dans la deuxième expression tu devrais échanger les noms de variable x et y pour y voir plus clair.
Tes deux intégrales sont l'intégrale de f(x)f(y)g(y)dxdy sur le triangle 0 <= x <= y <= e.
 \int_{y=x}^e g(y) dx dy<br /> = \int_{x=0}^e \int_{y=x}^e f(x)g(y) dx dy<br /> = \int_{x=0}^e \int_{y=0}^e {\mathbb 1}_{x \le y} f(x)g(y) dx dy \\<br /> = \int_{y=0}^e \int_{x=0}^e {\mathbb 1}_{x \le y} f(x)g(y) dx dy<br /> = \int_{y=0}^e \int_{x=0}^y f(x)g(y) dx dy<br /> = \int_{y=0}^e g(y) \int_{x=0}^y f(x) dx dy)
L'étape du milieu est justifiée par le théorème de fubini.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 23 Juin 2012, 14:55
friz a écrit:Bonjour à tous,
Je suis confronté à un problème. J'aurais besoin de déterminer si l'égalité A=B est correcte ou non pour un problème de physique. Voici les expressions de A et B.
Les fonctions f et g sont positives.
N'arrivant pas à établir analytiquement cette égalité, j'ai essayé d'intégrer numériquement A puis B (en essayant plusieurs types de fonctions : polynomiales, trigonométriques...). A prime abord, il semblerait que l'égalité soit vérifiée.
Maintenant, j'aimerais savoir si c'est vraiment le cas. Et si oui, comment peut on passer de l'expression de A à celle de B.
Merci d'avance pour votre aide.
L'intégration
se fait dans le triangle limité par l'axe des
et les droites
et
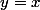
A tout point de ce domaine, où la fonction à intégrer vaut
f(y)g(y))
on peut associer un point symétrique par rapport à la droite
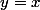
où la fonction vaut
g(x)f(y))
, c.a.d. a la même valeur.
Si on intègre dans ce domaine symétrique par rapport à
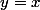
, c.a.d.
, l'intégrale aura la même valeur
-
friz
- Messages: 2
- Enregistré le: 21 Juin 2012, 15:44
-
par friz » 27 Juin 2012, 12:44
Merci à tous pour vos contributions. Elles répondent parfaitement à mon problème.
Ces deux notions (intégrales triangulaires et théorème de Fubini) m'échappaient totalement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
