Intégrales et Changements de variables

[ArtyB]

Bonsoir,

Pour calculer l'intégrale suivante en effectuant successivement deux changements de variables:
u=sin(x)
Puis (sin(u))*2^0,5=sin(d)
Il faut donc que j'arrive d'abord à transformer tous les cosinus en sinus n'est-ce pas ?
Ce que j'ai essayé de faire mais je me retrouve toujours avec un cosinus ici ou là...

[siger]

bonsoir

pourquoi 2 changements de variables?

cos(2x) = 1-2sin^2(x)
cos^3(x) dx =- (1-sin^2(x)) * d(sin(x))

[ArtyB]

Bonsoir,
Parce que c'est demandé dans l'énoncé.
Merci mais je ne comprends pas ça:
"cos^3(x) dx =- (1-sin^2(x)) * d(sin(x))"
Comment y arrivez vous ?

[mrif]

Bonsoir,
Parce que c'est demandé dans l'énoncé.
Merci mais je ne comprends pas ça:
"cos^3(x) dx =- (1-sin^2(x)) * d(sin(x))"
Comment y arrivez vous ?

Il y a une erreur de signe (erreur d'inattention)

[ArtyB]

Merci beaucoup !
C'était bien le cos(x) dx qui me posait problème et j'avais oublié qu'il fallait avoir d(sin(x)) après, merci !
Du coup on obtient integrale entre 0 et1/2 de racine(1-u²)du
et là il faut transformer les u tel que (sin(u))*(2^0,5)=sin(d).
En soit si on pose que u²=cos²(d) alors 1-u²=sin²(d) mais je ne suis pas sur que l'on puisse faire ça d'autant qu'ensuite il me faut une racine de 2 quelque part

[chan79]

Salut
On peut arriver au bout en faisant les changements de variables suivants:







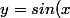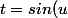pour arriver à

[fibonacci]

bonjour;

[Pisigma]

Bonjour,

En posant:



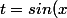et ensuite



Je trouve aussi:

[ArtyB]

Merci à vous pour vos réponses, mais le second changement de variable à effectuer est:
sin(d)=racine(2)*sin(u)

Je ne peux donc malheureusement pas appliquer les réponses que vous m'avez données

[siger]

re

cos(2x) = 1-2sin²(x)
cos³(x) = cos²(x) *cos(x) = (1-sin²(x)) *d(sin(x))

en posant sin(d) = V2*sin(x) on a d(sin(d) = V2*d(sin(x))
cos(2x) = 1-sin²(d) = cos²(d)
cos³(x) = (1-sin²(d)/2)*d(sin(d))
d'ou
........

[ArtyB]

EDIT: je trouvais le second changement de variables assez étrange aussi, j'ai envoyé un mail au CNED: coquille (une fois n'est pas coutume n'est-ce pas ?)

Donc on a le second changement de variable suivant:
racine(2)*u=sin(d)

[ArtyB]

Je ne comprends pas comment le faire en revanche, quelqu'un sait il ?

[siger]

RE

tu obtiens dans ton integrale un terme au denominateur en [( 1-2sin²(x)]^(1/2)
pour pouvoir eliminer la racine carrée tu poses 2sin²(x) = sin²(d)
ce qui conduit a
[(1-2sin²(x) ] = 1- sin²(d) = cos²(d)
d'ou un denominateur egal a cos(d)
.....

[ArtyB]

Oui mais ça c'est pour le premier changement de variable non ?
Maintenant que l'on a Integrale entre 0 et 1/2 de (1-u²)/(1-2u²)^1/2 du
il faut changer le u en sin(d)/racine de deux

[siger]

Re

premier changement de variable u= sin(x) : permet de transformer les cosinus en sinus

cos³(x)dx/(Vcos(2x)) devient (1-sin²(x)*d(sin(x))/(V (1-2sin²(x)) ou (1-u²)*du/(V1-2u²)

deuxieme changement de variable sin (d) = V2*sin(x) = V2*u : permet d'eliminer la racine carrée
d'ou
(1- u²) = 1-sin²(d)/2
du = (1/V2) cos(d) d(d)
1-2u² = 1-sin²(d) = cos²(d)

(1-u²)*du/(V(1-2u²)) devient (1/V2) (1-sin²(d)/2)*d(d)
.......

[Pisigma]

Oui mais ça c'est pour le premier changement de variable non ?
Maintenant que l'on a Integrale entre 0 et 1/2 de (1-u²)/(1-2u²)^1/2 du
il faut changer le u en sin(d)/racine de deux

L'écriture est un peu "bizarre" donc je remplace d par t





En tenant compte de



Je te laisse continuer...

[ArtyB]

Merci beaucoup à vous !
Donc après on a une primitive de (3+cos(2t)) qui est 3t+0,5*sin(2t)
D'où le résultat final: (1/(4V2)) *(3pi/4 + 0,5) ?

[Pisigma]

Merci beaucoup à vous !
Donc après on a une primitive de (3+cos(2t)) qui est 3t+0,5*sin(2t)
D'où le résultat final: (1/(4V2)) *(3pi/4 + 0,5) ?

Effectivement çà fait