Intégrale d'une fonction strictement positive

[AceVentura]

Bonsoir,

j'ai un petit doute. Est-ce si f est une fonction continue strictement positive sur [a,b] alors ? Merci par avance !

[Ericovitchi]

Même si elle n'est pas continue ça doit être vrai d'ailleurs.
l'intégrale c'est l'aire sous la courbe donc intuitivement ça va de soi.

[Nightmare]

C'est assez clair par construction par les sommes de Darboux !

[AceVentura]

Il va me falloir un argument moins costaud que les sommes de Darboux !

[Pythales]

Par la formule de la moyenne...

[Nightmare]

Il va me falloir un argument moins costaud que les sommes de Darboux !

Argument costaud? J'utilise juste la définition de l'intégrale de Riemann, c'est le minimum !

[AceVentura]

Par la formule de la moyenne...

Peux-tu préciser ?

[Arkhnor]

Salut.

Peux-tu préciser ?

Ben, l'intégrale est égale à , avec un point de , et cette quantité est strictement positive par hypothèse ...

Sinon, à la main : La fonction atteint son minimum sur , mettons en , alors pour tout 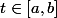, et donc , qui est là encore strictement positif.

La méthode avec les sommes de Darboux-Riemann me parait aussi très bonne, on utilise uniquement la définition de l'intégrale, et aucune propriété supplémentaire.

[AceVentura]

Parfait, merci beaucoup !

[Nightmare]

Sinon, à la main : La fonction atteint son minimum sur , mettons en , alors pour tout , et donc , qui est là encore strictement positif.

Salut :happy3:

Il y a pour moi un petit problème ici, tu utilises le fait que l'intégrale conserve l'ordre, or sauf erreur, cela utilise déjà le fait qu'une fonction positive est d'intégrale positive.

[Arkhnor]

Oui, c'est vrai, mais comme on veut prouver que l'intégrale d'une fonction strictement positive est strictement positive, on peut considérer le reste comme acquis.

Dans la preuve de la formule de la moyenne, on utilise aussi le fait que l'intégrale préserve l'ordre.

De toute manière, c'est ta méthode avec les sommes de Darboux qui est la meilleure, puisqu'elle a l'avantage de n'utiliser aucun résultat sur l'intégrale autre que la définition, mais apparemment, elle ne convient pas à AceVentura ...

Si on veut prouver une propriété de l'intégrale sans utiliser sa définition, il faut bien admettre une autre propriété, au risque de tourner en rond au moment de montrer cette dernière ...

[Dihtbscii]

[quote="Arkhnor"]Oui, c'est vrai, mais comme on veut prouver que l'intégrale d'une fonction strictement positive est strictement positive, on peut considérer le reste comme acquis.

Moé... moi je ne dirais même pas que ça utilise le fait que l'intégrale conserve l'ordre, c'est clairement un cas particulier de cette propriété!

[le-nguyen.hoang]

Quelqu'un saurait si cela reste vrai sans l'hypothèse de continuité ? Je reformule:

Soit f une fonction strictement positive intégrable au sens de Lebesgue sur un ensemble X de mesure non nulle. Est-ce que l'intégrale de f sur X est nécessairement strictement positive ?

[Arkhnor]

Bonjour.

Si est une fonction mesurable positive telle que , alors -pp. (résultat classique et simple qu'on peut trouver dans n'importe quel cours de théorie de la mesure)