Intégrale sur une courbe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
OveRdoZeuR
- Messages: 4
- Enregistré le: 09 Nov 2015, 21:46
-
 par OveRdoZeuR » 09 Nov 2015, 22:28
par OveRdoZeuR » 09 Nov 2015, 22:28
Bonsoir/Bonjour
J'ai un peu de mal avec une intégrale :
L'énoncé est :
Montrer que l'intégrale suivante est égale à zéro :
 d\ell$)
où
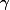
est l'ellipse

parcouru dans le sens anti-horaire.
Alors moi je commence par paramétrer ma courbe ,vu l'ellipse ,par :
 = 2 \cos(t)$)
 = \sin(t)$)
pour

Et puisque
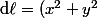^{1/2}$)
, j'arrive alors à
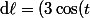^2 +1)^{1/2}$)
et au final mon intégrale de départ devient :
^3+\sin(t)^5)(3\cos(t)^2 +1)^{1/2} dt$)
Et là ... pouf :hein: , Wolfram me dit que c'est bien nul mais j'arrive pas du tout à le montrer ...
Vous auriez une idée ?
merci
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Nov 2015, 22:39
par Pythales » 09 Nov 2015, 22:39
OveRdoZeuR a écrit:Bonsoir/Bonjour
J'ai un peu de mal avec une intégrale :
L'énoncé est :
Montrer que l'intégrale suivante est égale à zéro :
 d\ell$)
où
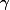
est l'ellipse

parcouru dans le sens anti-horaire.
Alors moi je commence par paramétrer ma courbe ,vu l'ellipse ,par :
 = 2 \cos(t)$)
 = \sin(t)$)
pour

Et puisque
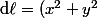^{1/2}$)
, j'arrive alors à
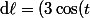^2 +1)^{1/2}$)
et au final mon intégrale de départ devient :
^3+\sin(t)^5)(3\cos(t)^2 +1)^{1/2} dt$)
Et là ... pouf :hein: , Wolfram me dit que c'est bien nul mais j'arrive pas du tout à le montrer ...
Vous auriez une idée ?
merci
N'est-ce pas

?
Mais je doute sur l'expression
dl)
-
OveRdoZeuR
- Messages: 4
- Enregistré le: 09 Nov 2015, 21:46
-
 par OveRdoZeuR » 09 Nov 2015, 22:48
par OveRdoZeuR » 09 Nov 2015, 22:48
Pythales a écrit:N'Est-ce pas

?
)^2 + sin(t)^2)^{1/2} =)
^2 + sin(t)^2)^{1/2} = (3 \cos(t)^2 + (\cos(t)^2 + sin(t)^2) )^{1/2} = (3 \cos(t)^2 + 1)^{1/2})
non ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Nov 2015, 22:50
par Pythales » 09 Nov 2015, 22:50
OveRdoZeuR a écrit:)^2 + sin(t)^2)^{1/2} =)
^2 + sin(t)^2)^{1/2} = (3 \cos(t)^2 + (\cos(t)^2 + sin(t)^2) )^{1/2} = (3 \cos(t)^2 + 1)^{1/2})
non ?
Non
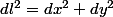
-
OveRdoZeuR
- Messages: 4
- Enregistré le: 09 Nov 2015, 21:46
-
 par OveRdoZeuR » 09 Nov 2015, 23:01
par OveRdoZeuR » 09 Nov 2015, 23:01
[quote="Pythales"]N'est-ce pas

?
Oui j'ai completement oublié de dériver c'est bien

-
OveRdoZeuR
- Messages: 4
- Enregistré le: 09 Nov 2015, 21:46
-
 par OveRdoZeuR » 09 Nov 2015, 23:13
par OveRdoZeuR » 09 Nov 2015, 23:13
Pythales a écrit:N'est-ce pas

?
Mais je doute sur l'expression
dl)
dl)
c'est l'énoncé que j'ai :/
l'intégrale à résoudre est maintenant :
^3+\sin(t)^5)(3\sin(t)^2 +1)^{1/2} dt$)
et j'arrive pas à trouver :help:
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Nov 2015, 16:21
par Pythales » 10 Nov 2015, 16:21
OveRdoZeuR a écrit:dl)
c'est l'énoncé que j'ai :/
l'intégrale à résoudre est maintenant :
^3+\sin(t)^5)(3\sin(t)^2 +1)^{1/2} dt$)
et j'arrive pas à trouver :help:
N'est ce pas

?
Sinon tu écris
\sqrt{3\sin^2t+1}\cos tdt+(1-\cos^2t)^2\sqrt{4-3\cos^2t}\sin tdt))
Dans la première, tu poses

et dans la 2ème

et tu as à intégrer
\sqrt{3u^2+1}du-(1-u^2)^2\sqrt{4-3u^2}du)
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 10 Nov 2015, 16:43
par Kolis » 10 Nov 2015, 16:43
OveRdoZeuR a écrit:dl)
c'est l'énoncé que j'ai :/
:
Mais qui est

?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
