Forcément, si quand on te dit "résidu", le premier truc que tu pense à écrire c'est en terme de limite d'un truc, ben tu risque souvent de pas arriver à grand chose...
Rappel : la
définition du résidu de f en a, c'est le coefficient en 1/(z-a) dans le développement en série de Laurent de f au voisinage de a.
(Et, évidement (et comme d'habitude en math), s'il y a un truc à savoir concernant une notion donnée, c'est sa définition.)Bref, si je disait que c'était une "application immédiate", ben c'est parce que c'est... une application immédiate : on te donne f sous forme de série de Laurent au voisinage de 0, donc pour avoir le résidu en 0 de
\cos(z)}{z^2})
,il suffit de dire que c'est le coeff. en
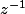
de
)
, c'est à dire en fait le coeff. en

de
\cos(z))
qui est en fait le coeff. en

de
)
vu que
\!=\!1\!+\!O(z^2))
De plus, dans ce cas de figure où la fonction F dont on cherche le résidu à un développement qui commence en
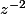
et pas en
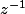
tu ne risque pas d'obtenir le résidu (c'est à dire le coeff. en
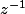
) par un simple calcul de limite vu que lorsque
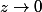
, c'est le coeff en z^{-2} qui va systématiquement l'emporter.
Bref, ta façon de calculer le résidu ne risque pas de marcher dans un cas pareil (et elle ne marchera jamais dans les cas où il y a des termes en
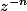
avec
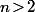
)