Cercles et contour

[sylvain231]

Bonjour par "contour" j'entends une suite de points liée par des segments, fermée et ne se recoupant pas.
Je cherche le plus petit cercle qui entoure ce contour sans le couper d'une part, et d'autre part le plus grand cercle contenu dans ce contour sans en déborder.
Merci de m'aider
Bien cordialement

[lyceen95]

Pour la 1ère question, voici une solution qui va utiliser des méthodes 'informatiques' plutôt que mathématiques.
Admettons que tu aies 20 points. Le cercle optimal va forcément passer par 3 de ces 20 points. Tu peux recenser tous les triplets possibles (20x19x18/6=1140 triplets). Pour chaque triplet (A,B,C), tu recherches le centre du cercle circonscrit de ce triangle, et tu calcules le rayon de ce cercle, et tu vérifies que le cercle en question enveloppe bien tous les points de la figure. Si oui, tu mémorises ce cercle, sauf si on avait déjà trouvé un cercle valide, plus petit.

[sylvain231]

merci ça marche mais c'est en O(n^4) donc pas très optimisé !

Voici mon code attention ça utilise ma classe Circle mais on peut facilement deviner son utilisation, c'est du C++ :

Code: Tout sélectionner

Circle cercleCirconscrit(std::vector<cv::Point> contour,int precision) {
   bool br;
   Circle res = Circle(0, Point(-1, -1));
   double minRadius = 9999999999;
   for (int i = 0; i < contour.size(); i += precision) {
      cout << "i=" << i+1<<"/"<< contour.size()<<endl;
      for (int j = 0; j < contour.size(); j+= precision) {
         if (i != j) {
            for (int k = 0; k < contour.size(); k+= precision) {
               if (k != i && k != j) {
                  br = false;
                  Circle c(contour[i], contour[j], contour[k]);
                  //vérif si tous les points du contour sont dans le cercle
                  Point P = c.getCenter();
                  double R = c.getRadius();
                  for (int l = 0; l < contour.size(); l += precision) {
                     if (distanceP(P, contour[l]) > R)
                     {
                        br=true;
                        break;
                     }
                  }
                  if (!br && R<minRadius) {
                     res = c;
                     minRadius = R;
                  }
               }
            }
         }
      }
   }
   return res;
}


[lyceen95]

Oui, c'est basique de chez basique.
Voici quand même une optimisation qui va diviser le temps de traitement par 6. Dans ta 1ère version, tu testais le cercle basé sur le triangle (1,2,3), puis un peu plus tard le cercle basé sur le triangle (1,3,2), puis ... ...

Code: Tout sélectionner

Circle cercleCirconscrit(std::vector<cv::Point> contour,int precision) {
   bool br;
   Circle res = Circle(0, Point(-1, -1));
   double minRadius = 9999999999;
   for (int i = 0; i < contour.size(); i += precision) {
      cout << "i=" << i+1<<"/"<< contour.size()<<endl;
      for (int j = i+1; j < contour.size(); j+= precision) {
            for (int k = j+1; k < contour.size(); k+= precision) {
                  br = false;
                  Circle c(contour[i], contour[j], contour[k]);
                  //vérif si tous les points du contour sont dans le cercle
                  Point P = c.getCenter();
                  double R = c.getRadius();
                  for (int l = 0; l < contour.size(); l += precision) {
                     if (distanceP(P, contour[l]) > R)
                     {
                        br=true;
                        break;
                     }
                  }
                  if (!br && R<minRadius) {
                     res = c;
                     minRadius = R;
                  }
               }
         }
   }
   return res;
}

Et on peut encore probablement améliorer un peu, en inversant les 2 tests (si le rayon du cercle envisagé est supérieur au meilleur rayon trouvé jusque là, inutile de tester si tous les points sont dans le cercle)

Code: Tout sélectionner

Circle cercleCirconscrit(std::vector<cv::Point> contour,int precision) {
   bool br;
   Circle res = Circle(0, Point(-1, -1));
   double minRadius = 9999999999;
   for (int i = 0; i < contour.size(); i += precision) {
      cout << "i=" << i+1<<"/"<< contour.size()<<endl;
      for (int j = i+1; j < contour.size(); j+= precision) {
            for (int k = j+1; k < contour.size(); k+= precision) {
                  br = false;
                  Circle c(contour[i], contour[j], contour[k]);
                  //vérif si tous les points du contour sont dans le cercle
                  Point P = c.getCenter();
                  double R = c.getRadius();
                  if R < minRadius {
                    for (int l = 0; l < contour.size(); l += precision) {
                       if (distanceP(P, contour[l]) > R)
                       {
                          br=true;
                          break;
                       }
                    }
                    if (!br) {
                       res = c;
                       minRadius = R;
                    }
               }
         }
   }
   return res;
}

S'il y a vraiment beaucoup de points, on doit pouvoir faire un premier nettoyage, pour éliminer des points qui seraient forcément inutiles. En particulier, remplacer le polygone par son enveloppe convexe est un traitement peu couteux, et qui peut utile ici.

Si le nombre de points est élevé (disons 50 ou plus ), tu peux aussi faire un premier traitement, très simple :
pour i = 1 a 25,
- calculer la distance entre le point i et le point i+25.
- et garder le max de toutes ces valeurs
C'est à dire, en gros, prendre 2 points diamétralement opposés, à la hache, et calculer la distance entre ces 2 points, et retenir la plus grande des valeurs trouvées.
On sait que le cercle cherché aura un diamètre supérieur à ce nombre.

Donc dans le traitement précédent, si le R= c.getRadius() est plus petit que la moitié de ce diamètre de référence (fréquent dès qu'on prend 3 points consécutifs ou presque), on sait que le cercle ne pourra pas contenir tous les autres points. Inutile de tous les tester.

[lyceen95]

Pour l'autre question, la recherche du plus grand cercle inscrit, on peut avoir la même approche.
Dans le premier cas, on partait d'un constat : le plus petit cercle circonscrit passe par 3 points du contour.
Pour la 2ème question, ça devient : Le plus grand cercle inscrit est tangent à 3 segments.

On va donc procéder pareil , 3 boucles imbriquées, qui nous donnent 3 segments. Recherche du cercle tangent à ces 3 segments. Test si ce cercle est plus grand que la meilleure solution trouvée jusque là, et test si le cercle est bien 'intérieur' au polygone.
Le principe est similaire, mais les formules sont certainement beaucoup plus compliquées.

[sylvain231]

oui je vois pas comment trouver le cercle tangeant à 3 segments et si un cercle est à l'intérieur d'un polygone, ce ne sont pas des questions triviales

[sylvain231]

pour le cercle tangeant à 3 segments j'ai une idée, continuer les segments jusqu'à tracer un triangle puis calculer le cercle inscrit à ce triangle

[lyceen95]

Dans le cas d'un rectangle a*b avec a<b, la solution est un cercle de diamètre a, et on peut mettre ce cercle où on veut dans le rectangle. En particulier, il y a 2 solutions optimales, avec ce cercle tangent à 3 côtés du rectangle. La propriété de départ reste vraie.

Le cercle tangent à 3 segments, c'est effectivement compliqué. En fait, c'est le cercle tangent à 3 droites. Rien ne dit que les points de contact sont sur les segments. Si les points de contacts ne sont pas sur les segments, j'imagine que le cercle ne sera pas retenu pour tel ou tel critère.
Partant de 3 segments, on a 3 droites, on a donc un triangle (un nouveau triangle, les 3 sommets ne font pas partie des points de notre liste initiale, sauf cas particulier). Le centre du cercle recherché est le point d'intersection des 3 médiatrices.

[sylvain231]

oui tu as raison

[sylvain231]

j'ai trouvé cela pour un cercle dans un polygone mais ne comprends pas ; https://cs.stackexchange.com/questions/ ... -a-polygon

[lyceen95]

Oui, j'ai édité mon message ... la méthode pour trouver le cercle à partir de 3 segments est celle-là.

[sylvain231]

ah je viens de comprendre le forum, c'est bon j'ai tout en main, demain je fais un code

[sylvain231]

en gros et en termes simples : si chacune des distances du centre du cercle à chacun des sommets du polygone est supérieure ou égale au rayon du cercle alors le cercle est dans le polygone

[lyceen95]

Non, c'est faux. Les 2 sommets d'un segment peuvent être à l'extérieur du cercle, alors que le segment coupe le cercle.

[lyceen95]

Attention, à partir de 3 droites, il y a en fait 4 points qui permettent de bâtir des cercles tangents à ces 3 droites. Un des cercles est intérieur au triangle formé par ces 3 droites, et les autres sont extérieurs à ce cercle.
Quand on parle d'intersection des bissectrices, à partir de 2 droites, il y a 2 bissectrices.
Et on ne s'intéresse pas toujours au cercle qui est à l'intérieur du triangle.
Si on part d'un dodécagone régulier ou quasiment, si on prend 3 segments consécutifs ( ou avec un faible trou entre ces segments), le cercle qui nous intéresse est extérieur au triangle formé par ces 3 droites.

Dans ces questions sur des polygones, souvent, c'est utile d'avoir comme contrainte : les points du polygone sont donnés dans l'ordre direct ( les points arrivent dans l'ordre inverse des aiguilles d'une montre)

[sylvain231]

Pour ton avant-dernier message, as-tu un schéma montrant cette exception car pour moi ça marche ? Pour ton dernier message je n'ai pas compris.

[lyceen95]

Tu disais : si chacune des distances du centre du cercle à chacun des sommets du polygone est supérieure ou égale au rayon du cercle alors le cercle est dans le polygone
Non.
Dessine un cercle, par exemple le cercle d'équation x²+y²=140 ; place les 2 points (10,7) et (10,-7) ; ils sont à l'extérieur du cercle, mais le segment reliant ces 2 points coupe le cercle. Avec ces 2 points, à la place de 140, je pouvais prendre n'importe quel nombre entre 100,001 et 148,999.

Pour l'autre question, regarde ce lien : https://fr.wikipedia.org/wiki/%C3%89l%C3%A9ments_remarquables_d%27un_triangle
Regarde le premier dessin, il y a un cercle orange, et il y a 3 arcs de cercle également en orange, qui sont extérieurs au triangle ABC. Ces 4 cercles sont tangents aux 3 droites AB, AC, et BC.

Maintenant, partons de 30 points par exemple ... 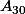; supposons que ces points forment un polygone convexe. Si on regarde les segments , on a 3 droites qui s'appuient sur ces 3 segments, on a un triangle qui est dessiné par ces 3 droites, mais ce triangle sera certainement à l'extérieur du polygone initiale.
Alors que si on prend les segments , le triangle obtenu contient généralement le polygone, et parmi les 4 cercles possibles, celui qui nous intéresse est bien celui qui est à l'intérieur du triangle.

[sylvain231]

le cercle d'équation x²+y²=140 a pour rayon 11.83 donc les 2 points (10,7) et (10,-7) sont dans le cercle, mais je vois ce que tu veux dire en prenant un cercle de rayon 9 on s'en aperçoit

[lyceen95]

10²+7²=100+49=149, qui est supérieur à 140. Donc les points (10,7) et (10,-7) sont à l'extérieur du cercle de centre O et de rayon

[sylvain231]

donc il faut prendre les 4 cercles en orange et pas seulement le cercle inscrit pour notre algo ? car le cercle inscrit il suffit de prendre les 3 intersections des droites