Intégrale définie

[tetraedre]

Bonjour à tous et bonne année !

Quequ'un peut il m'aider à résoudre l'exercice suivant ?

[catamat]

Bonjour

Je ne suis pas allé au bout mais on peut factoriser le dénominateur



ce qui permet de décomposer la fonction rationnelle...

[tetraedre]

OK pour calculer une primitive , mais comment tenir compte du fait que le paramètre a est racine d'une équation du troisième degré ?

[tetraedre]

Oups , je pense que la décomposition en facteurs de catamat est fausse ....
Ce serait plutot (x-a)(x²+ax + a²+1)

[Rdvn]

Bonjour

Les deux expressions sont vraies car
a^2+1 = -1/a
sachant
a^3+a+1 = 0 (par définition de a)

Ceci dit je quitte le sujet, faute de temps, souhaitant qu'un autre membre soit plus disponible
Bon courage

[phyelec]

Bonjour,

on a une équation du troisième degré de la forme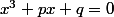 avec q et p réels dont on connait une racine à savoir a et p=q=1. Sauf erreur de ma part en utilisant la méthode de méthode de Bombelli et en disant que =a on obtient les autres racines :

et


on peut donc écrire et faire un développement en élément simple.

[tetraedre]

Il y a une seule racine réelle , x2 et x3 sont des racines complexes...

[phyelec]

oui

[tetraedre]

J’ai calculé la primitive pour une valeur de a = - 0.6823.
Cela me donne comme résultat pour l’intégrale la valeur 0.4993.
Je pense que la solution cherchée est ½ ( confirmée par un graphique Géogebra ), mais je ne sais pas le montrer…
Il,y a probablement une méthode élégante sans passer par la primitive ?

[phyelec]

pour ma part, j'ai conduit le calcul en posant ( j'ai peut-être tort) :



A+B-C=0 ( je n'ai pas calculé A,B et C)

je trouve ( sauf erreur de ma part) : A ln(2) - (B-C) ln(|-a|).

[tetraedre]

Je ne comprend pas trop le raisonnement de Phyelec :
A,B,C sont arbitraires ?
Au final cela donne quoi ?

[catamat]

Personnellement en partant de la factorisation que je donnais plus haut j'obtiens cette décomposition :

avec
où j'utilise le fait que

Pour l'integrale de la deuxième fraction utiliser un changement de variable

[tetraedre]

Avec mes notations l'intégrale donne :



Je vais me résoudre à admettre cette valeur approchée bien que je pense que la valeur exacte est 1/2...

[catamat]

Perso je pense que c'est bon, car ayant essayé avec une v.a de a ayant 10 décimales -0.6823278038 ou même 15 chiffres, je reste sur 0,499269