Intégrale dans un domaine
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kaya
- Membre Naturel
- Messages: 91
- Enregistré le: 03 Aoû 2005, 15:33
-
 par kaya » 29 Avr 2006, 17:00
par kaya » 29 Avr 2006, 17:00
Salut à tous!
là j'ai une petite grande question sur intégrale qui me dérange qqfois:
posons
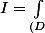}f(x,y,z)dxdydz)
la question: que signifie vraiment I (pour f ou/et pour (D)) du point de vu géométrique (s'il y en a)?
parce que quand on fait
dx)
on sait que c'est la surface limité par f, x=a, x=b et y=0.
:hein: :hein:
merci d'avance pour réponse.
-
zorg
- Membre Naturel
- Messages: 78
- Enregistré le: 21 Avr 2006, 09:17
-
 par zorg » 29 Avr 2006, 17:03
par zorg » 29 Avr 2006, 17:03
iL s'agit d'un volume dans R^4.
-
kaya
- Membre Naturel
- Messages: 91
- Enregistré le: 03 Aoû 2005, 15:33
-
 par kaya » 29 Avr 2006, 17:10
par kaya » 29 Avr 2006, 17:10
soit disons R^3
-
zorg
- Membre Naturel
- Messages: 78
- Enregistré le: 21 Avr 2006, 09:17
-
 par zorg » 29 Avr 2006, 20:45
par zorg » 29 Avr 2006, 20:45
Comprends pas ?
Quand on intégre f(x) une fonction d'une variable sur un segment (1 dimension) on obtient l'aire d'une surface de R^2
Quand on intégre f(x,y) une fonction de 2 variables sur un domaine de R^2 (2 dimensions) on obtient un volume de R^3 (le volume de base le domaine et limité par la surface z=f(x,y))
Quand on intégre f(x,y,z) une fonction de 3 variables sur un "domaine" de R^3 (3 dimensions) on obtient un -disons- hypervolume de R^4.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités