Intégrale de contour dans plan complexe

[Marcet003]

Bonjour,

Je cherche à calculer l'intégrale suivante : où 0 < p < 1

J'étends l'intégrant sur le plan complexe :

Le corrigé choisi un contour d'intégration qui englobe les singularités en et contourne le pt. de ramification en z = 0 comme sur l'image suivante :

Ma question porte sur le sens du contour interne autour du point de ramification en z = 0. Le corrigé tourne dans le sens horaire depuis le segment A vers le segment B. De sorte que en sommant les contributions des deux segments A et B, on obtient : (cf. image ci-dessous)



Moi j'ai essayé de tourner dans l'autre sens pour la boucle i.e dans le sens anti-trigonométrique. Donc je pars du segment B et je tourne de pour arriver sur le segment A. Les contributions des segments A et B me donnent respectivement :





En sommant mes contributions, j'ai donc ce qui n'est pas la même chose que le corrigé.

Je serai très reconnaissant si on pouvait m'aiguiller sur ce que ma démarche a de faux...

Merci d'avance,...

[GaBuZoMeu]

Bonsoir,
On veut que l'intégrale sur le segment A corresponde à . Donc la détermination de sur le domaine à l'intérieur du contour est bien où est l'argument entre et on arrive bien du côté de B avec .
La détermination choisie de n'a rien à voir avec le sens dans lequel on tourne sur la boucle autour de l'origine. Le sens dans lequel on tourne est d'ailleurs indiqué par les flèches : c'est le sens des aiguilles d'une montre, qui est le sens anti-trigonométrique

[Marcet003]

Bonjour,

C'est justement ce sens dans lequel on tourne qui n'est pas clair pour moi.

Dans le cas du corrigé (celui que tu reprends), ce qui me perturbe c'est que on devrait comme tu dis parcourir la boucle interne dans le sens anti-trigo (selon schéma). Cependant, il me semble que le corrigé la parcours dans le sens trigo, lorsque , avec le qui garde la mémoire d'une rotation dans le sens trigonométrique.

Donc, ce que je me suis dis, c'est que je commence par parourir le segment B, je tourne ensuite dans le sens anti-trigonométrique pour arriver sur le segment A et je remplace pour garder la mémoire d'une rotation dans le sens anti-trigo.

Peut-être mon problème est-il plus clair maintenant ?

[GaBuZoMeu]

Tu n'as pas saisi ce que j'ai mis en gras dans mon message. Il y a deux choses complètement différentes :
1°) Le sens dans lequel on parcourt le bord du domaine pour appliquer le théorème des résidus. On le parcourt en laissant à sa gauche l'intérieur du domaine. Donc pour la boucle de rayon , on la parcourt dans le sens des aiguilles d'une montre.
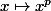
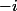
2°) La détermination de à l'intérieur du domaine. On veut que cette détermination aboutisse à sur l'axe réel positif quand on arrive par le haut (du côté du segment A). En suivant cette détermination par continuité dans le domaine, on arrive à quand on arrive sur l'axe réel positif par le bas. Il y a deux pôles de la détermination de dans le domaine en et . Avec cette détermination de et donc de , les résidus en ces pôles sont respectivement et .
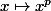
Il semble que tu veuilles prendre une autre détermination de pour que cette détermination aboutisse à sur l'axe réel positif quand on arrive par le bas. Cette détermination est égale à la précédente multipliée par et aboutit à quand on arrive sur cet axe réel par le haut. Les résidus aux pôles de la détermination correspondante de sont aussi multipliés par . Au bout du bout, on arrivera exactement au même calcul.