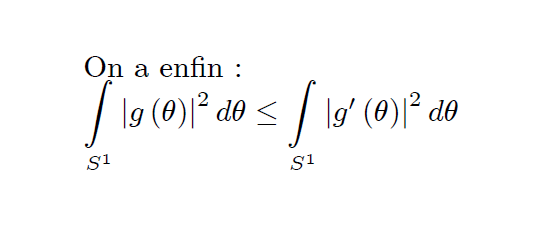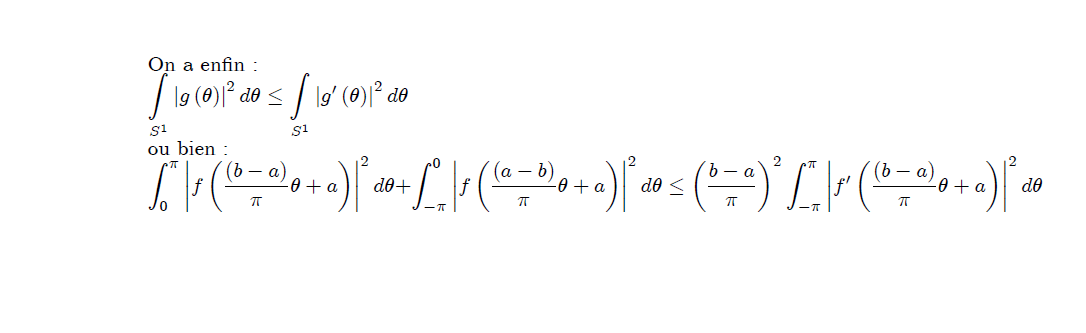L'inégalité de Wirtinger.
14 messages
- Page 1 sur 1
Re: L'inégalité de Wirtinger.
Salut,
C'est quoi qui te bloque (les indics te donnent la piste et il n'y a qu'à la suivre...)
C'est quoi qui te bloque (les indics te donnent la piste et il n'y a qu'à la suivre...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: L'inégalité de Wirtinger.
Où est l'image ?
Super la réponse, on sent que t'as envie d'avancer. Essaie d'être plus optimiste et essaie de faire quelque chose.
algharib a écrit:C'est défficile
Super la réponse, on sent que t'as envie d'avancer. Essaie d'être plus optimiste et essaie de faire quelque chose.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: L'inégalité de Wirtinger.
Tu n'as évidement pas à "calculer" ces intégrales (comment voudrait tu le faire sans plus d'info. sur f ?)
Ce que tu as à faire, c'est le lien entre les intégrales définissant les) et celle définissant les
et celle définissant les ) de façon à trouver le lien entre les deux intégrales correspondante (via la relation de Plancherel).
de façon à trouver le lien entre les deux intégrales correspondante (via la relation de Plancherel).
Ce que tu as à faire, c'est le lien entre les intégrales définissant les
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: L'inégalité de Wirtinger.
Ben314 a écrit:Tu n'as évidement pas à "calculer" ces intégrales (comment voudrait tu le faire sans plus d'info. sur f ?)
Ce que tu as à faire, c'est le lien entre les intégrales définissant leset celle définissant les
de façon à trouver le lien entre les deux intégrales correspondante (via la relation de Plancherel).
J'ai démontré que :
Re: L'inégalité de Wirtinger.
Avec ça et les relations de Plancherel, c'est fini.
Attention quand même au fait que, si k=0, très clairement, la relation que tu donne ne risque pas d'être valable...
Attention quand même au fait que, si k=0, très clairement, la relation que tu donne ne risque pas d'être valable...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: L'inégalité de Wirtinger.
Ben314 a écrit:Avec ça et les relations de Plancherel, c'est fini.
Comment ?
Re: L'inégalité de Wirtinger.
Pourquoi la première somme est-elle forcément plus petite que la deuxième ?
(et tu peut même donner les cas d'égalité qui correspondent en fait aux cas d'égalité dans l'inégalité isopérimétrique)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :