Inégalité triangulaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 24 Sep 2007, 20:12
par magnum » 24 Sep 2007, 20:12
bonjour,
j'ai problème avec l'inégalité triangulaire généralisée,
l Z1+Z2+Z3+...Zk l < ou égale à lZ1l+lZ2l+...+lZkl
en fait j'ai trouvé la condition nécéssaire et suffisante à l'égalité , " il faut et il suffit que Zi/Zj soit un réel positif mais je n'arrive pas à la démontrer .
Merci
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 24 Sep 2007, 20:32
par Alpha » 24 Sep 2007, 20:32
En fait il faut et il suffit que les Zi soient sur une même demi-droite d'origine 0, ce qui revient à dire que Zi/Zj est un réel positif pour tous i,j tq Zj est non nul, mais il y a une façon plus efficace de le dire : il existe

tel que pour tout i,
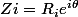
. Si on écrit les choses ainsi, il est immédiat que c'est une condition suffisante.
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 24 Sep 2007, 20:41
par magnum » 24 Sep 2007, 20:41
OK, merci pour la piste de l'écriture expo, mais comment démontrer que c'est une condition nécéssaire? T'as une idée ?
Merci
désolé pour la faute entre nécéssaire et suffisante ...
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 24 Sep 2007, 20:54
par magnum » 24 Sep 2007, 20:54
la condition suffisante, est , en effet triviale mais pour prouver que c'est une condition néncéssaire peux-tu m'aider ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Sep 2007, 21:19
par fahr451 » 24 Sep 2007, 21:19
bonsoir
récurrence
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 24 Sep 2007, 21:23
par magnum » 24 Sep 2007, 21:23
j'y ai bien sûr pensé , mais quelle serait la phrase à démontrer dans ce cas ?
"l z1 + z2 + ...+zk l = l z1 l + l z2 l + l z3 l +...+l zk l ssi ...?
merci fahr .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Sep 2007, 21:28
par yos » 24 Sep 2007, 21:28
Si
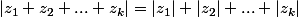
, alors
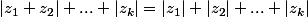
(en effet le premier membre est coincé entre les deux membres de départ). Donc
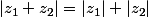
et tu as
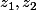
colinéaires de même sens.
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 24 Sep 2007, 21:42
par magnum » 24 Sep 2007, 21:42
[quote="yos"]Si
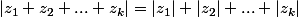
, alors
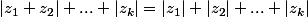
(en effet le premier membre est coincé entre les deux membres de départ).
peux-tu expliquer un peu plus ce passage, merci.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Sep 2007, 21:56
par yos » 24 Sep 2007, 21:56
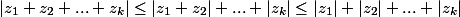
C'est l'inégalité triangulaire.
Maintenant, si le premier membre est égal au troisième, celui du milieu sera égal aux deux autres.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
 tel que pour tout i,
tel que pour tout i, 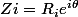 . Si on écrit les choses ainsi, il est immédiat que c'est une condition suffisante.
. Si on écrit les choses ainsi, il est immédiat que c'est une condition suffisante.