Inégalité suite de fonctions

par **Marcet003** » 27 Sep 2024, 16:40

Bonjour,

Pour

une suite de Cauchy de fonctions dans

. Je n'arrive pas à voir d'où vient l'inégalité suivante :

.

Merci d'avance,...

par **alm** » 27 Sep 2024, 17:47

Bonjour, tu as parlé la suite

mais on voit

, je pense que ta question fera mieux de contenir une définition de ce que tu note

.

par **Marcet003** » 27 Sep 2024, 18:02

C'est simplement la limite de la suite par complétude de

par **issoram** » 29 Sep 2024, 13:57

Bonjour,

Soit

Ainsi

On devrait pouvoir conclure non?

par **Ben314** » 29 Sep 2024, 19:23

Salut,
Perso, j'aurais écrit que, pour tout

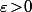
, il existe un

tel que

donc

Et cette inégalité étant vraie pour tout

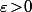
, celà signifie que

Et en fait, ce truc c'est jamais qu'un résultat classique concernant les suites numériques : si une suite réelle

est convergeante alors

.