Inégalité des accroissements finis pour les fonctions à vale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 27 Déc 2008, 12:15
par legeniedesalpages » 27 Déc 2008, 12:15
Bonjour,
je cherche à montrer cette inégalité:
Soit
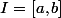
un intervalle un intervalle non-vide dans

et
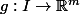
,
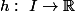
deux fonctions continues sur

, dérivables sur l'intérieur de

. Si on a
||\leq h'(t))
pour tout
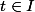
, alors
-g(a)||\leq h(b)-h(a))
.
Je ne vois pas trop l'astuce, j'ai essayé d'appliquer le thm des accroissements finis un peu à toutes les sauces mais je n'aboutis sur rien.
Merci pour votre aide.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 27 Déc 2008, 12:18
par XENSECP » 27 Déc 2008, 12:18
Hum...En fait tu décomposes par composante et applique l'IAF sur chacune des composantes qui sont des fonctions I->R qui vérifie les hypothèses de l'IAF classique :)
 par legeniedesalpages » 27 Déc 2008, 12:29
par legeniedesalpages » 27 Déc 2008, 12:29
désolé je viens de corriger,

est à valeurs dans

.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 27 Déc 2008, 12:32
par XENSECP » 27 Déc 2008, 12:32
oui c'est mieux ^^
tu dis simplement que
 = \sum_{k=1}^{m} g_{k}(x))
et puis tu applique au
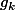
l'IAF classique

 par legeniedesalpages » 27 Déc 2008, 12:46
par legeniedesalpages » 27 Déc 2008, 12:46
si j'applique ainsi l'IAF classique, je peux affirmer que pour tout entier
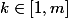
,
il existe
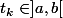
tel que
|\leq L_k)
,
l'IAF donne
-g_k(a)}{b-a}|\leq L_k)
mais que choisir comme
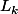
? je prends
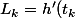)
?
Je ne vois pas non plus comment passer de
-g_k(a)}{b-a}|)
à
-g(a)||)
sans connaître l'expression de la norme.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Déc 2008, 13:10
par Joker62 » 27 Déc 2008, 13:10
Haileau ;)
C'est beaucoup plus subtil que ça en fait.
Je te donne les grandes lignes vite fait.
On se ramène à l'étude sur [0;1]
On pose A_e = { x [0;1] | ||g(x)-g(0)|| - ( h(x) - h(0 ) - ex <= e }
On remarque que A_e est non vide ; Par continuïté on sait qu'il existe un n>0 tel que [0;n] soit contenu dans A_e
En remarquant que A_e est fermé et en posant a_e son sup, on a que a_e A_e
Il suffit donc de prouver que a_e = 1
Tu supposes que a_e < 1 et en bossant avec les formules de Taylor tu aboutiras à une contradiction
Voili Voilou, c'est beaucoup plus subtile quand même :o
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Déc 2008, 13:19
par Joker62 » 27 Déc 2008, 13:19
Oui on est pas forcément dans R^n donc bon parler de composante c'était un peu dangereux.
Si t'as des soucis pour la fin demande donc j'ai encore le cours juste à côté de moi lol :D
 par legeniedesalpages » 27 Déc 2008, 13:30
par legeniedesalpages » 27 Déc 2008, 13:30
J'écris la formule de Taylor-Young:
}_{>\varepsilon} = \underbrace{\psi(a_{\varepsilon})}_{\leq \varepsilon}+h[\psi'(a_{\varepsilon})+o(1)])
lorsque
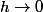
,
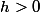
.
Si j'ai bien saisi, il faudrait montrer que
+h[\psi'(a_{\varepsilon})+o(1)]\leq \varepsilon)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Déc 2008, 13:42
par Joker62 » 27 Déc 2008, 13:42
Donc en gros, tu appliques Taylor sur g et sur h en a_e on obtient pour h très petit
g(a_e + h) - g(a_e) = h.g'(a_e) + he1(h)
h(a_e + h) - h(a_e) = h.h'(a_e) + he2(h)
avec h assez petit pour que ||e1(h)|| < e/2 et |e2(h)| < e/2
On a || g(a_e + h) - g(a_e) || <= h ||g'(a_e)|| + he/2 <= h.h'(a_e) + he/2
On remplace h.h'(a_e) par la valeur trouver au dessus
on a donc
<= h(a_e+h) - h(a_e) - he2(h) + he/2
Maintenant e/2 - e2(h) < e d'où
|| g(a_e + h) - g(a_e) || <= h(a_e + h) - h(a_e) + he
Maintenant tu utilises le fait que a_e A_e
Tu fais une vulgaire inégalité triangulaire et tu trouveras que a_e + h A_e ce qui est absurde
Voili Voilou
J'file au lavage ;)
 par legeniedesalpages » 27 Déc 2008, 14:18
par legeniedesalpages » 27 Déc 2008, 14:18
ok tout est clair maintenant, merci beaucoup.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités