Indicatrice d'Euler (comportement asymptotique)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 18 Aoû 2010, 19:01
par GeorgeB » 18 Aoû 2010, 19:01
Bonjour, en révisant l'arithmétique sur des exercices de Terminale C je suis tombé sur un exercice concernant l'indicatrice d'Euler, on a déjà montré que :
=n(1-\frac{1}{p_1})...(1-\frac{1}{p_r}))
On me demande alors de montrer que la limite de l'indicatrice d'Euler en l'infini est l'infini.
Je dois donc montrer que pour tout entier naturel N il existe N' tel que n>N' => phi(n)>N
Comment dois-je faire ?
Merci d'avance
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Aoû 2010, 19:41
par girdav » 18 Aoû 2010, 19:41
Bonjour,
on peut montrer que
 \geq \sqrt n)
pour

.
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 18 Aoû 2010, 21:06
par GeorgeB » 18 Aoû 2010, 21:06
Tout d'abord merci de votre réponse.
Cependant, je n'y parviens pas, pouvez vous m'indiquer comment procéder ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 09:21
par Doraki » 19 Aoû 2010, 09:21
Si tu cherches à montrer qu'il y a un nombre fini de nombres n tels que phi(n) <= N,
tu peux commencer à regarder phi(n) lorsque n admet un facteur premier >= N+2. Ca élimine déjà plein de nombres d'un coup.
Pour ceux qui restent, ta formule permet d'avoir phi(n) >= n*a pour une certaine constante a.
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 09:58
par GeorgeB » 19 Aoû 2010, 09:58
Désolé, je ne vois pas comment montrer que phi(n)>A lorsque n possède un facteur premier>=A+2...
Pour la suite , j'avais déjà essayer de triturer la formule , mais ce sont des facteurs tous plus petit que 1 donc bon, ça n'avance pas trop.
Désolé je ne vois pas :--:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 10:01
par Doraki » 19 Aoû 2010, 10:01
C'est quoi, p1, p2, ..., pr dans la formule ?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 10:09
par GeorgeB » 19 Aoû 2010, 10:09
Ce sont les diviseurs premiers de n.
Le truc c'est que j'aimerais minorer cette formule mais je peut pas, a part avec 2 pour chaque p_k et en ces cas là on a :
phi(n)>n(1/2)^r mais ça ne sert a rien ...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 10:14
par Doraki » 19 Aoû 2010, 10:14
Tu n'aurais pas une formule qui exprime phi(n) comme un produit de nombres entiers en fonction de la décomposition de n en facteurs premiers ?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 10:20
par GeorgeB » 19 Aoû 2010, 10:20
sisi c'est
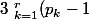p_k^{q_k-1})
mais je ne vois pas ce que l'on en tire franchement puisque on est obligé de le minorer par 2 pour chaque p_k ....
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 12:59
par Doraki » 19 Aoû 2010, 12:59
Avec cette formule, si n a un facteur premier >= N+2, t'arrives pas à montrer que phi(n) > N ?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 13:43
par GeorgeB » 19 Aoû 2010, 13:43
Si si j'y arrive,
C'est pour la deuxième partie que je n'y arrive pas .. celle ou on a pas de facteur >= N+2
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 14:15
par Doraki » 19 Aoû 2010, 14:15
Ah ben dans ce cas il reste quoi comme possibilités pour les facteurs premiers ?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 14:41
par GeorgeB » 19 Aoû 2010, 14:41
Oui, je sais ce sont que des facteurs premiers inférieurs ou égaux à N+1 seulement dans les deux formules ça ne m'est d'aucune utilité puisque dans la première ça me dit simplement que
 \le \frac{N+2}{N+1})
or on a ici majorer, et moi je veut minorer ...
Avec la seconde on minore également. Bref, on peut minorer par 2, mais ce n'est pas suffisant et donc je n'ai rien. La seule formule qui ressemble à la votre c'est en prenant p1,p2...pr les nombres premiers qui divisent n :
 \ge n(\frac{1}{2})^r)
mais je peut pas montrer que ça dépasse n'importe quelle valeur N.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 14:52
par Doraki » 19 Aoû 2010, 14:52
r il peut être grand comment ?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 14:59
par GeorgeB » 19 Aoû 2010, 14:59
Bah justement je sais pas, je sais qu'il ne peut exéder n/2 mais je pense qu'on peut faire mieux, mais je vois pas :cry:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Aoû 2010, 15:02
par Doraki » 19 Aoû 2010, 15:02
J'te rappelle que n est un nombre qui n'a aucun facteur premier plus grand que N+1
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 19 Aoû 2010, 15:06
par GeorgeB » 19 Aoû 2010, 15:06
Ah oui, il sera de toute manière majoré par N donc ... on a ce qu'on veut :we:
Merci énormément !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités