Indépendance fonction n-périodique et une période
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hollycran
- Messages: 6
- Enregistré le: 27 Oct 2021, 16:22
-
 par Hollycran » 06 Nov 2021, 10:17
par Hollycran » 06 Nov 2021, 10:17
Bonjour, j'ai une première question d'un exercice et je n'arrive pas à apporter la preuve nécessaire.
Soit n ∈ N∗
On note E l'ensemble des fonctions n-périodiques de Z dans C :
E = {f : Z → C | ∀k ∈ Z, f(k + n) = f(k)}.
1) Montrer que la somme de n valeurs consécutives d'une fonction n-périodique sur Z est indépendante de
la période sur laquelle est effectuée cette somme, c'est-à-dire que :
∀f ∈ E , ∀p ∈ Z,
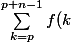=\sum ^{n-1}_{k=0}f(k)\])
J'ai essayé de le prouver en faisant la récurrence sur Z mais je ne vois pas comment aboutir.
Merci
Modifié en dernier par
Hollycran le 07 Nov 2021, 18:08, modifié 1 fois.
-
catamat
- Habitué(e)
- Messages: 1369
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 06 Nov 2021, 10:29
par catamat » 06 Nov 2021, 10:29
Bonjour
En posant , k'=k-p, cela doit marcher...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2021, 19:15
par Ben314 » 06 Nov 2021, 19:15
Salut,
Pour moi, ce type d'exo., si tu y arrive pas, c'est que tu raisonne de façon trop compliqué et que tu n'a pas l'habitude de prendre des exemple.
Imagine que je pose (quasi) la même question en te disant qu'on a (par exemple) 10 nombres A,B,C,D,E,F,G,H,I,J tels que
F=A
G=B
H=C
I=D
J=E
(c'est à dire une période de longueur 5)
puis je te demande de montrer que
A+B+C+D+E = B+C+D+E+F = C+D+E+F+G = D+E+F+G+H = E+F+G+H+I+J
ça te semble compliqué ou pas ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 06 Nov 2021, 22:18
par lyceen95 » 06 Nov 2021, 22:18
Un peu dans le même registre que Ben314.
Quand tu lis cette propriété qu'on te demande de montrer, sur cet exercice bien précis, quelle est ta réaction ?
1- Ben oui, bien sûr, cette propriété est vraie, mais je ne sais pas comment la démontrer.
2. Ah ? Ah oui, en effet, c'est vrai. Mais comment la démontrer.
2- Ah ? Cette propriété est vraie ? Bon, s'ils le disent, on va leur faire confiance. Tentons de la démontrer.
3- Autre chose, à préciser.
-
Hollycran
- Messages: 6
- Enregistré le: 27 Oct 2021, 16:22
-
 par Hollycran » 07 Nov 2021, 00:18
par Hollycran » 07 Nov 2021, 00:18
C'est vrai que ça paraît tout de suite plus facile à montrer. Pour ma part j'essaie aussi de m'approprier la fonction par un exemple (j'ai pris la fonction cosinus) et ensuite je cherche comment la prouver. Ici, on me dit montrer que donc la première idée qui me vient à l'esprit est la récurrence. Si je reprends la première solution proposée je me retrouve avec
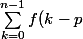=\sum ^{n-1}_{k=0}f(k)\])
et je n'arrive toujours pas à voir où et comment aboutir...
-
tulipe
- Membre Naturel
- Messages: 56
- Enregistré le: 06 Juin 2021, 16:07
-
 par tulipe » 07 Nov 2021, 04:00
par tulipe » 07 Nov 2021, 04:00
(Si jamais ça peut aider, sinon c'est à oublier)
Comme la fonction est n-périodique au lieu de garder p il suffit de garder la classe de p modulo n, afin de se ramener à des nombres compris en 0 et n-1 :
p=p'+tn (avec p' compris entre 0 et n-1)
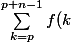=\sum ^{p'+tn+n-1}_{k=p'+tn}f(k)\])
en posant j=k-tn cela donne
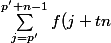=\sum ^{p'+n-1}_{j=p'}f(j))
on retombe sur une somme analogue sauf que cette fois ci p' est compris entre 0 et n-1.
Il ne reste qu'une dernière étape à franchir pour obtenir le résultat.
-
Maxymyze
- Membre Naturel
- Messages: 52
- Enregistré le: 04 Nov 2021, 21:33
-
 par Maxymyze » 07 Nov 2021, 04:35
par Maxymyze » 07 Nov 2021, 04:35
C'est bien compliqué pour ce que c'est vos histoires (à moins que je ne me trompe)
L'image d'une fonction ou d'une suite périodique sur la totalité du domaine de définition, c'est l'image de la fonction ou de la suite périodique sur n'importe laquelle de ses périodes.
Si l'image est de cardinal fini, comme dans le cas qui nous occupe (dans une période, qui est de diamètre fini, il n'y a qu'un nombre fini d'antécédents, puisque ce sont des entiers), la somme des éléments de l'image est définie, et la constance de l'image, en tant qu'ensemble, entraîne la constance de la somme.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Nov 2021, 16:31
par Ben314 » 07 Nov 2021, 16:31
Perso., si je devait absolument écrire autre chose que "c'est complètement évident", ben je pense que j'écrirais ça :
Si, pour tout
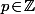
, on pose
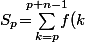)
alors on a
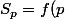\!+\!\!\!\!\sum^{p+n-1}_{k=p+1}\!\!\!\!f(k)=f(p\!+\!n)\!+\!\!\!\!\sum^{p+n-1}_{k=p+1}\!\!\!\!f(k)\ \ \ \ \text{du fait de la p\'eriodicit\'e de } f)
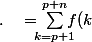=S_{p+1})
Ce qui montre que la suite
_{p\in\Z})
est constante et donc que
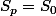
pour tout

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Hollycran
- Messages: 6
- Enregistré le: 27 Oct 2021, 16:22
-
 par Hollycran » 07 Nov 2021, 18:09
par Hollycran » 07 Nov 2021, 18:09
C'est bien compliqué pour au final peu de chose mais je comprends très bien la rédaction apporté par Ben et elle est au final plutôt intuitive. Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
